단순한 선형 회귀와 다중 회귀 사이의 가정의 유일한 차이는 다중공선성 문제입니다.
다중공선성이란 무엇입니까?
독립 변수 간에 높은 상관 관계가 있을 때, 우리는 일반적으로 다중공선성 또는 상호 상관의 문제가 존재한다고 말합니다. 다중공선성을 감지는 여러 가지 방법이 있습니다. 그중 한 가지 방법은 아래와 같이 상관 행렬을 사용하는 것입니다.
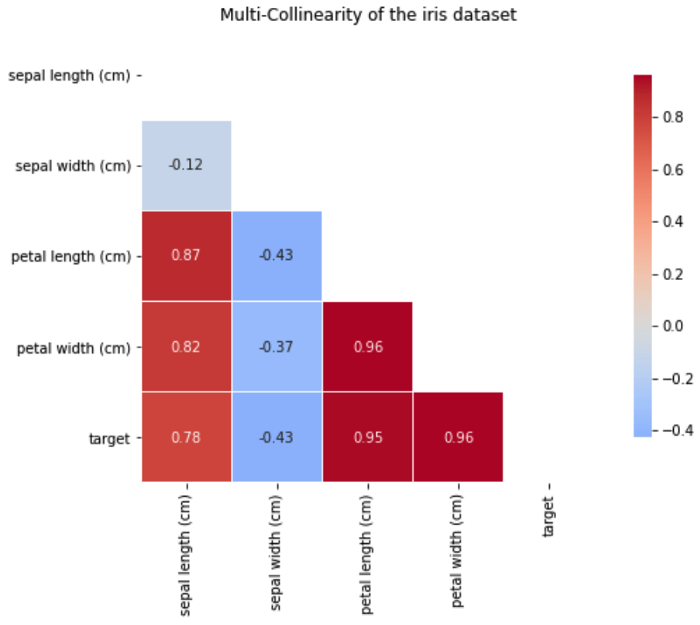
매트릭스는 꽃 잎 길이(petal length, cm)와 꽃 잎 너비(petal width, cm) 사이의 높은 상관 관계를 명확하게 보여줍니다.
다중공선성을 발견하는 또 다른 방법은 분산 인플레이션 계수(VIF)를 계산하는 것입니다.


모델 해석
일반적으로 모델 해석입니다. 목표는 독립 변수 중 하나에서 변경이 발생할 때 종속의 영향 또는 변경을 이해하는 것입니다. 예를 들어 다음 방정식이 있습니다:

주택 가격을 계산한다고 가정해 보겠습니다.

매개 변수 추정치(베타 계수)를 계산하여 주택 가격과 독립 변수 사이의 관계를 얻을 수 있습니다.
Squares가 다른 변수와 무관하다고 가정하면 증가하면 집의 가격이 beta2에 의해 상승 할 것입니다.
객실 수(number of rooms)와 층 수(number of floors) 사이의 강한 상관 관계로 인해 다중공선성이 있다고 가정해 봅니다.
이를 대처하지 않으면 매개 변수 추정치가 잘못되어 기능의 통계적 중요성을 손상시킬 수 있습니다.
여기에서 보다 신뢰할 수 있는 추정치를 얻으려면 독립 변수 중 하나를 제거해야합니다(효과를보다 시각적으로 표현하려면 여기를 클릭하십시오).
모델 예측
분석 목표가 해석보다는 예측 일 때, 다른 시나리오가 발견됩니다.
이 점은 Kutner (2005)의 책 적용 선형 통계 모델에 요약되어 있습니다.
다음의 예를 통해 설명해보겠습니다.

두 개의 독립적 인 변수 X1과 X2는 완벽하게 상관 관계가 있습니다.
이는 일반적으로 신뢰할 수 없는 매개 변수 추정치를 의미하지만 회귀 모형으로 표현하면 추정치는 다음과 같습니다.

방정식은 데이터에 완벽하게 맞지만 다음과 같이 변경해도 문제 없습니다(테이블에서 숫자를 삽입하고 직접 확인해보십시오).

첫 번째 방정식은 X2가 목표 변수에 큰 영향을 미치는 반면, 두 번째 방정식은 완전히 다른 스토리를 알려줍니다.
이것은 우리가 매개 변수 추정치를 해석하지 않는 한 데이터에 완벽하게 맞는 모델을 쉽게 가질 수 있고, 심지어 예측을 할 수 있음을 의미합니다.
다시 말해, 목표가 예측 인 기계 학습 컨텍스트에 대한 데이터 세트를 준비 할 때는 열을 제거 할 필요가 없습니다.
즉, 매개변수 추정치에 큰 관심이 없고 예측에 더 포커스를 맞춘 기계학습은 다중공선성이 발생하더라도 별 문제가 없음을 의미합니다.
[참고 원문]
https://towardsdatascience.com/why-multicollinearity-isnt-an-issue-in-machine-learning-5c9aa2f1a83a
'Data Analysis' 카테고리의 다른 글
| [ML] Shapley Value의 머신러닝 적용 (0) | 2023.01.13 |
|---|---|
| [ML] SHAP 소개 (3) | 2023.01.13 |
| [통계] 통계 기초 (0) | 2023.01.12 |
| 다중공선성이란? 제거하는 방법은? (0) | 2023.01.11 |
| 공간 클러스터링: 종류와 사용 (0) | 2021.08.20 |




댓글