SHAP는 기계 학습 모델의 예측을 설명하는 수학적 방법입니다. 게임 이론을 기반으로 하며 예측에 대한 각 기능의 기여도를 계산하여 기계 학습 모델의 예측을 설명하는 데 사용할 수 있습니다. SHAP는 가장 중요한 변수를 찾고, 변수가 모델 예측에 미치는 영향을 확인할 수 있습니다. SHAP는 그 이면에 있는 수학을 설명하지 않고는 완전히 이해할 수 없습니다. 이에 여기에서는 수학 식 뒤에 숨겨진 직관을 설명하고 각 주제에 대한 몇 가지 예를 제공함으로써 가능한 한 수학적 설명을 단순화하려고 노력합니다. 또한 작동 방식을 완전히 이해하는 데 도움이 되도록 Python을 사용하여 처음부터 다양한 SHAP 알고리즘을 구현합니다.
Python의 SHAP 라이브러리
여기에서는 SHAP 값을 계산하는 데 사용할 수 있는 다양한 방법을 연구하고 각 방법은 Python으로 구현됩니다. 그러나 이 코드는 알고리즘이 어떻게 작동하는지 보여주는 데만 사용되며 실제 응용 프로그램에는 효율적이지 않습니다. Python의 SHAP 라이브러리를 사용하여 모델의 SHAP 값을 효율적으로 계산할 수 있으며 여기에서는 이 라이브러리를 사용하는 방법을 간략하게 보여줍니다. 또한 이를 사용하여 각 섹션에 제공된 Python 스크립트의 출력을 검증합니다.
Explaining the predictions of a model
대부분의 기계 학습 모델은 대상을 예측하도록 설계되었습니다. 여기서 예측의 정확도가 매우 중요하지만 모델이 특정 예측을 수행하는 이유도 이해해야 합니다. 따라서 모델을 설명하는 도구가 필요합니다. 이는 모델의 예측과 모델이 해당 예측을 생성하는 데 사용한 데이터 인스턴스의 구성 요소 간의 관계를 질적으로 이해하고 싶다는 것을 의미합니다. 이러한 구성 요소는 데이터 인스턴스의 기능(표 형식 데이터 집합이 있는 경우)이거나 이미지의 픽셀 집합 또는 텍스트 문서의 단어일 수 있습니다. 이러한 구성 요소의 존재(또는 부재)가 예측에 어떤 영향을 미치는지 확인하려고 합니다.
선형 회귀 또는 결정 트리와 같은 기계 학습의 일부 모델은 해석 가능합니다. 여기서 해석 가능성은 예측을 위해 모델이 사용하는 프로세스를 인간이 이해하는 것이 얼마나 쉬운지를 나타냅니다. 예를 들어 의사 결정 트리 분류기를 플로팅하면 특정 예측을 수행하는 방법을 쉽게 이해할 수 있습니다. 반면 딥러닝 모델은 블랙박스와 같아서 이러한 모드가 어떻게 예측을 하는지 쉽게 이해할 수 없습니다. SHAP는 개별화된 모델에 구애받지 않는 설명자입니다. 모델에 구애받지 않는 방법은 설명할 모델이 블랙박스이고 모델이 내부적으로 어떻게 작동하는지 모른다고 가정합니다. 따라서 모델에 구애받지 않는 방법은 설명할 모델의 입력 데이터와 예측에만 액세스할 수 있습니다. 개별화된 모델 불가지론적 설명자는 해석 가능한 모델 자체입니다. 설명자는 특정 데이터 인스턴스에 대해 설명할 모델의 동일한 예측을 대략적으로 만들 수 있습니다(그림 1). 이제 우리는 이 해석 가능한 모델이 원래 모델이 단일 특정 예측을 만드는 데 사용하는 프로세스를 모방하고 있다고 가정할 수 있습니다. 따라서 해석 가능한 모델이 원래 모델을 설명할 수 있다고 말합니다. 요약하면 SHAP는 모델이 내부적으로 어떻게 작동하는지 알지 못하더라도 기계 학습 모델을 설명할 수 있으며 게임 이론의 개념을 사용하여 이를 달성할 수 있습니다. 따라서 이를 이해하려면 먼저 Shapley 값에 익숙해져야 합니다.

Shapley values
Shapley 값은 1951년 Lloyd Shapley가 소개한 게임 이론의 수학적 개념입니다. 그는 이 연구로 나중에 노벨 경제학상을 수상했습니다. 1부터 M까지 번호가 매겨진 M명의 플레이어가 있는 협력 게임이 있고 F가 플레이어 집합을 나타내므로 F = {1, 2, … . . , M}. 연합 S는 F의 부분 집합으로 정의되며(S ⊆ F), 빈 집합 ∅도 플레이어가 없는 연합이라고 가정합니다. 예를 들어 플레이어가 3명인 경우 가능한 연합은 다음과 같습니다.

집합 F도 연립(coalition)이며 우리는 그것을 대연정(grand coalition)이라고 부릅니다. M 플레이어의 경우 2M 연합이 있음을 쉽게 알 수 있습니다. 이제 각 연합을 실수로 매핑하는 함수 v를 정의합니다. v는 특성 함수라고 합니다. 따라서 각 연합 S에 대해 수량 v(S)는 실수이며 연합 S의 가치라고 합니다. 이는 해당 연합의 플레이어가 함께 행동할 경우 얻을 수 있는 총 이득 또는 집단적 보상으로 간주됩니다. 빈 연합에는 플레이어가 없기 때문에 다음과 같이 가정할 수 있습니다.

이제 우리는 M 플레이어와의 연합 게임에서 각 플레이어의 총 보상에 대한 기여도가 무엇인지 알고 싶습니다. 즉, 플레이어들 사이에서 총 이득을 나누는 가장 공정한 방법은 무엇입니까?
예제를 사용하여 이 문제를 해결하는 방법을 보여줄 수 있습니다. 5명의 플레이어가 있는 게임이 있다고 가정합니다. 따라서 F = {1, 2, . . . , 5}. 플레이어를 한 번에 하나씩 빈 세트에 추가하여 대 연합 F를 형성한다고 가정합니다. 따라서 새 플레이어를 추가할 때마다 F의 새로운 연합을 형성합니다. 예를 들어 먼저 빈 세트에 {1}을 추가합니다. 세트이므로 현재 플레이어 세트는 F의 연합인 {1}입니다. 그런 다음 {2}를 추가하고 현재 세트는 연합 {1,2}이며 F={1, 2, 3, 4, 5}. 각 플레이어가 현재 플레이어 세트에 추가되면 이전 연합의 총 이득이 증가합니다. 예를 들어 현재 집합이 {1, 2}인 경우 총 이득 v({1, 2}). {3}을 추가한 후 총 이득은 v({1, 2, 3})가 됩니다. 이제 현재 연합에 대한 {3}의 기여도가 현재 연합({3} 포함)과 {3}을(를) 포함하지 않은 이전 연합의 값 간의 차이라고 가정할 수 있습니다.

{3}을 추가한 후 {4} 및 {5}를 추가할 수 있으며 총 이득도 변경됩니다. 그러나 {3}의 기여도에는 영향을 미치지 않으므로 이전 방정식은 여전히 {3}의 기여도를 제공합니다(그림 2). 그러나 여기에는 문제가 있습니다. 플레이어 추가 순서도 중요합니다.

이 플레이어가 회사의 부서 직원이라고 가정합니다. 회사는 먼저 {1}을(를) 고용합니다. 그런 다음 기술이 부족하다는 것을 파악하고 {2}을(를) 고용합니다. {2}을(를) 고용한 후 회사의 총 이익은 $10000만큼 증가하며 이는 {1}에 추가될 때 {2}의 기여입니다. {3}을(를) 고용한 후 {3}의 기여는 $2000에 불과합니다. 또한 직원 {2} 및 {3}의 스킬 세트가 유사하다고 가정합니다. 이제 직원 {3}은(는) 자신이 더 일찍 고용되었더라면 {2}의 동일한 기여도를 갖게 되었을 것이라고 주장할 수 있습니다. 즉, {1}에 추가될 때 {3}의 기부금도 $10000가 될 수 있습니다. 따라서 각 플레이어의 기여도를 공정하게 평가하려면 대연합을 형성하기 위해 추가되는 순서도 고려해야 합니다.
사실 플레이어 {i}의 기여도를 공정하게 평가하려면 F의 모든 순열을 형성하고 각 순열에서 {i}의 기여도를 계산한 다음 이러한 기여도의 평균을 취해야 합니다. 예를 들어 F={1, 2, 3, 4, 5}의 가능한 순열은 다음과 같습니다.
그리고 이 순열에서 {3}의 기여도는 다음과 같습니다.
다른 순열은 다음과 같습니다.

그리고 이 순열에서 {3}의 기여도는 다음과 같습니다.

다른 순열은 다음과 같습니다.

그리고 이 순열에서 {3}의 기여도는 다음과 같습니다.

특성 함수 v는 순열이 아니라 연합을 인수로 취한다는 점에 유의하는 것이 중요합니다. 연합은 집합이므로 요소의 순서는 중요하지 않지만 순열은 정렬된 요소 모음입니다. [3,1,2,4,5]와 같은 순열에서 3은 첫 번째 플레이어이고 5는 팀에 추가된 마지막 플레이어입니다. 따라서 각 순열에 대해 요소의 순서는 총 이득에 대한 기여도를 변경할 수 있지만 순열의 총 이득 또는 가치는 순서가 아닌 요소에만 의존합니다. 그래서:

따라서 각 순열 P에 대해 먼저 {i} 이전에 추가된 플레이어 연합의 가치를 계산해야 합니다. 이 연합을 S라고 하자. 그러면 S에 {i}를 더하여 형성된 연합의 가치를 계산해야 하며, 이 연합을 SU{i}라고 한다. 이제 ϕᵢ로 표시된 플레이어 {i}의 기여도는 다음과 같습니다.

대연정 F의 총 순열 수는 |F|! (여기서 |F|는 집합 F의 요소 수를 의미합니다.) {i}에 대한 기여도의 평균을 얻기 위해 기여도의 합을 그것으로 나눕니다.

그림 3에서 볼 수 있듯이 일부 순열은 연합 S 및 SU{i}가 동일하므로 동일한 기여도를 갖습니다. 따라서 방정식을 계산하는 더 쉬운 방법입니다. 식1은 기여도의 고유 값만 계산하고 반복 횟수를 곱한다는 것입니다. 그러기 위해서는 각 연합에서 얼마나 많은 순열을 형성할 수 있는지 파악해야 합니다. F-{i}를 플레이어 {i}를 제외한 모든 플레이어의 집합이라고 하고 S는 F-{i}의 연합(S ⊆ F-{i}) 중 하나입니다. 예를 들어 F={1,2,3,4,5} 및 {i}={3}의 경우
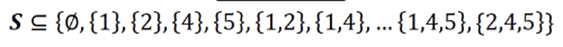
S의 요소 수는 |S|로 표시되며 |S|! 이러한 요소로 순열. 예를 들어 S={1,2}이면|S|=2이고, 2!=2 순열: [1, 2] 및 [2, 1]이다(그림 4). 우리는 또한 S로부터 형성된 각 순열의 가치가 v(S)임을 압니다. 이제 S에서 형성된 각 순열의 끝에 플레이어 {i}를 추가합니다. 결과 순열의 가치는 모두 연합 SU{i}에 속하므로 v(SU{i})입니다. 집합 F는 F의 모든 요소를 포함하는 순열을 형성하기 위해 SU{i}의 끝에 추가될 수 있는 SU{i}의 요소를 제외한 나머지 요소 |F|-|S|-1개를 가집니다. 따라서 다음이 있습니다. (|F|-|S|-1)! 입니다. SU{i}에 추가하는 방법.
예를 들어, 이전 예에서 F의 나머지 요소는 {4} 및 {5}입니다. 따라서 (|F|-|S|-1)= (5–2–1)!=2 즉, 나머지 요소를 사용하여 대 연합을 형성하는 두 가지 방법이다. 결과적으로 S! (|F|-|S|-1)! {i}가 S의 순열 뒤에 오고 나머지 플레이어가 {i} 뒤에 오는 F의 순열을 형성하는 방법.

각 순열의 총 이득에 대한 {i}의 기여도는 다음과 같습니다.
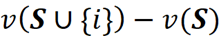
그리고 이러한 모든 순열의 총 이득에 대한 {i}의 총 기여는 다음과 같습니다.
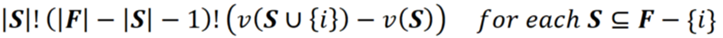
지금까지 우리는 F에서 하나의 가능한 연합 S의 순열을 다루고 총 이익에 대한 {i}의 총 기여도를 계산했습니다. 이제 F의 모든 순열에서 {i}의 기여도 합계를 얻기 위해 F-{i}의 다른 연합에 대해 동일한 절차를 반복할 수 있습니다.
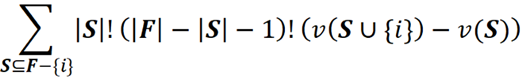
마지막으로 |F|! 따라서 F의 모든 순열의 총 이득에 대한 {i}의 평균 기여도는 이전 항을 |F|!로 나누어 얻을 수 있습니다.
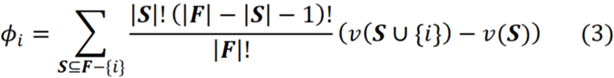
여기서 ϕᵢ는 F의 모든 순열에서 {i}의 평균 기여도인 요소 {i}의 Shapley 값이라고 합니다. 이것은 F의 모든 플레이어의 총 이득에 대한 플레이어 {i}의 수학적으로 공평한 몫입니다. 앞에서 살펴본 것처럼 각 연합 S는 S! (|F|-|S|-1)! 순열을 만들 수 있습니다. 순열의 총 수는 |F|!이므로 다음과 같이 쓸 수 있습니다.
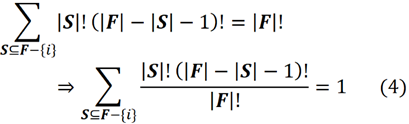
Shapley 값에는 다음 속성이 있어야 합니다.
1-효율성: 모든 플레이어의 기여도 합계는 총 이득을 제공해야 합니다.
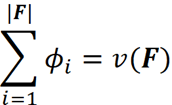
1- 대칭: i와 j가 i와 j를 포함하지 않는 모든 연합 S에 대해 v(S ∪ {i}) = v(S ∪ {j})인 경우 ϕᵢ=ϕⱼ . 가능한 모든 연합에 동일한 이득을 제공한다면 동일한 기여도를 가져야 합니다.
2- 더미: i가 i를 포함하지 않는 모든 연합 S에 대해 v(S) = v(S ∪ {i})인 경우 ϕᵢ = 0입니다. 연합이면 그 기여도는 0입니다.
3- 가산성: u와 v가 게임에 대한 두 가지 다른 특성 함수라고 가정합니다. 플레이어 i의 기여도를 각각 ϕᵢ(u) 및 ϕᵢ(v)라고 합니다(여기서 ϕᵢ(u)는 ϕᵢ이 u의 함수임을 의미합니다). 그러면 ϕᵢ(u + v) = ϕᵢ(u) + ϕᵢ(v)가 됩니다. 예를 들어 이 속성을 명확히 합시다. 직원 팀이 두 개의 다른 프로젝트에서 작업하고 각 프로젝트에 대한 직원의 총 보수와 기여도가 다르다고 가정합니다. 그런 다음 이러한 프로젝트를 결합하면 결합된 프로젝트에서 직원의 기여도는 각 프로젝트에 대한 기여도의 합계입니다.
방정식 3의 Shapley 값이 이러한 속성을 만족한다는 것을 쉽게 보여줄 수 있습니다.
SHAP는 기계 학습 모델의 예측을 설명하는 수학적 방법입니다. 게임 이론의 개념을 기반으로 하며 예측에 대한 각 기능의 기여도를 계산하여 기계 학습 모델의 예측을 설명하는 데 사용할 수 있습니다. SHAP는 가장 중요한 기능과 모델 예측에 미치는 영향을 결정할 수 있습니다. SHAP는 수학적 주제이며 그 이면에 있는 수학을 설명하지 않고는 완전히 이해할 수 없습니다. 그러나 수학적 주제 뒤에 숨겨진 직관을 설명하고 각 주제에 대한 몇 가지 예를 제공함으로써 가능한 한 수학적 주제를 단순화하려고 노력합니다. 독자는 옵션 섹션이나 부록에 제시된 더 어려운 주제를 건너뛸 수도 있습니다. 또한 작동 방식을 완전히 이해하는 데 도움이 되도록 Python을 사용하여 처음부터 다양한 SHAP 알고리즘을 구현합니다.
'Data Analysis' 카테고리의 다른 글
| [ML] SHAP의 수학적 설명 (0) | 2023.01.14 |
|---|---|
| [ML] Shapley Value의 머신러닝 적용 (0) | 2023.01.13 |
| [통계] 통계 기초 (0) | 2023.01.12 |
| 다중공선성이란? 제거하는 방법은? (0) | 2023.01.11 |
| 기계학습과 다중공선성 (0) | 2023.01.11 |




댓글