플레이어의 Shapley 값을 기계 학습 모델의 기능과 어떻게 연관시킬 수 있습니까? 그림 5와 같이 N개의 행과 M개의 기능이 있는 데이터 세트가 있다고 가정합니다.
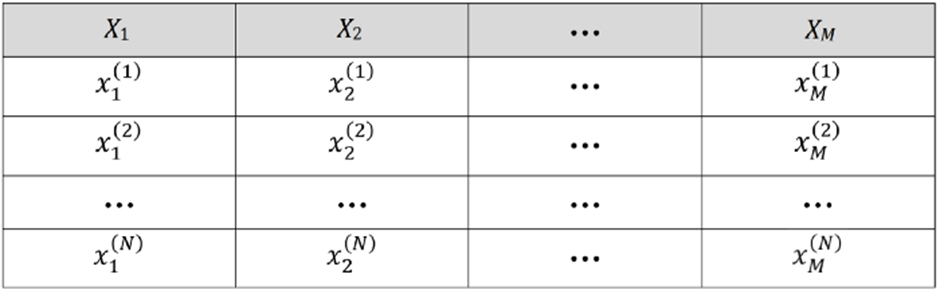
여기서 Xᵢ는 데이터 세트의 i번째 특징이고 xᵢ⁽ʲ⁾는 j번째 예에서 i번째 특징의 값이며 y⁽ʲ⁾는 j번째 행의 대상입니다. 기능 값은 M 요소가 있는 행 벡터로 표시되는 기능 벡터를 형성할 수 있습니다.

여기에 X₁=x₁, X₂=x₂, ... X_M=x_M이 있습니다(선형 대수학에서 벡터는 일반적으로 열 벡터로 간주되지만 이 문서에서는 행 벡터라고 가정합니다). 특징 벡터는 데이터 세트의 j번째 행이 될 수도 있습니다. 이 경우 다음과 같이 작성할 수 있습니다.

또는 데이터 세트에 없는 테스트 데이터 포인트일 수 있습니다(이 문서에서 굵은 글꼴 소문자(예: x)는 벡터를 나타냅니다. 굵은 대문자(예: A)는 행렬을 나타내고 소문자(예: x₁)는 스칼라 값을 나타냅니다). 데이터 세트의 특징은 (X₁)와 같이 대문자로 표시됩니다. 쌍(x⁽ʲ⁾, y⁽ʲ⁾)을 이 데이터 세트의 학습 예제라고 합니다. 이제 모델을 사용하여 이 데이터 세트를 학습할 수 있습니다.
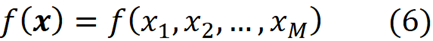
이 함수는 x의 모든 요소에 적용됨을 의미하는 특징 벡터 x를 사용합니다. 예를 들어 선형 모델의 경우 다음이 있습니다.

따라서 각 x 값에 대해 모델 예측은 f(x)입니다. 앞서 언급했듯이 이 특징 벡터 x는 훈련 데이터 세트의 인스턴스 중 하나이거나 훈련 데이터 세트에 존재하지 않는 테스트 데이터 인스턴스 중 하나일 수 있습니다. 예를 들어, 이 선형 모델을 사용하여 교육 예제 중 하나의 대상을 예측할 수 있습니다.
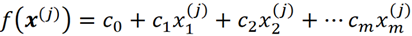
따라서 f(x⁽ʲ⁾)는 데이터 세트의 j번째 행에 대한 모델 예측이며, f(x⁽ʲ⁾)와 y⁽ʲ⁾의 차이는 j번째 훈련 예시에 대한 모델의 예측 오차입니다.
기계 학습 모델이 연합 게임이고 M 기능이 이 게임의 M 플레이어라고 가정할 수 있습니다. 하지만 이 게임의 특징적인 기능은 무엇이어야 할까요? 첫 번째 추측은 f(x) 자체일 수 있습니다. 그러나 특성 함수는 방정식 1을 충족해야 합니다. 즉, 플레이어가 없을 때 총 이득은 0입니다. features(플레이어)가 없을 때 f(x)를 어떻게 평가할 수 있습니까? Feature가 게임의 일부가 아닌 경우 현재 값을 알 수 없으며 해당 feature의 값을 모른 채 모델의 대상을 예측하려고 합니다. 게임에 feature이 없다는 것은 feature의 현재 값을 알 수 없다는 의미입니다. 이 경우 예측을 위해 훈련 세트만 사용할 수 있습니다. 여기에서 훈련 예제 샘플(또는 모두)에 대한 f(x⁽ʲ⁾)의 평균을 최선의 추정치로 취할 수 있습니다. 따라서 feature이 없을 때의 예측은 다음과 같습니다.
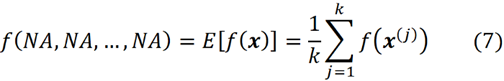
여기서 NA는 사용할 수 없는 feature을 의미합니다(따라서 여기서는 f의 매개변수를 사용할 수 없음). 또한 훈련 데이터 세트(k≤N)에서 k 데이터 인스턴스(특징 벡터)를 샘플링했습니다. 이제 대연정의 특징적인 기능을 다음과 같이 정의합니다.

feature이 없으면 방정식 7을 사용하여 다음을 얻습니다.

이 특성 함수는 이제 방정식 1을 만족하고 대 연합 F={X₁, X₂,…, X_M}의 가치를 제공할 수 있습니다. 그러나 방정식 3을 사용할 수 있으려면 F-{i}의 연합 가치도 필요합니다. 함수 f를 원래 인수의 하위 집합에 어떻게 적용할 수 있습니까? 두 가지 방법으로 할 수 있습니다. 첫째, 원래 기능의 하위 집합에서만 동일한 모델(동일한 하이퍼파라미터 사용)을 재교육할 수 있습니다. 예를 들어 연합 S에 다음 기능이 포함되어 있는 경우:
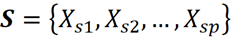
그런 다음 fₛ(xₛ)라고 하는 이러한 기능에 대한 f의 한계 값이 필요합니다.
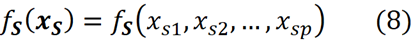
여기서 xₛ는 S에 있는 기능의 값만 포함하는 벡터입니다(연합은 기능으로 구성되지만 함수는 이러한 기능의 값을 취함). fₛ(xₛ)를 얻기 위해 연합 S에 있는 기능에 대해 동일한 유형의 모델을 재교육하거나 원래 함수 f를 사용하여 fₛ를 계산할 수 있습니다. 기능이 S에 없으면 현재 값을 알 수 없으며 NA(사용할 수 없음)로 대체할 수 있음을 의미합니다.

예를 들어 F={X₁, X₂, X₃, X₄, X₅}이고 연합 S={X₁, X₂, X₅}인 경우 특성 X₃ 및 X₄의 현재 값을 알 수 없습니다. 그래서:

여기서는 f로 표현되는 모델이 NA 값을 처리할 수 있다고 가정합니다. 따라서 이 연합의 가치는 다음과 같습니다.
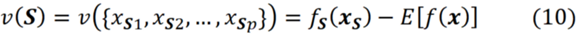
여기서 fₛ(xₛ)는 연합 S에 있는 기능에 대해 모델을 재훈련하거나 방정식 9에서 얻습니다. 예를 들어, F={X₁, X₂, X₃, X₄, X₅} 및 S={X₁, X₂ X₅}, S의 가치는 다음과 같습니다.
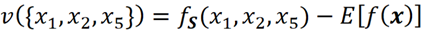
이제 방정식 3과 방정식 10을 사용하여 기능 Xᵢ의 Shapley 값을 계산할 수 있습니다.

이 방정식에서 방정식 3과 일치하도록 ϕₓᵢ를 작성해야 합니다. 그러나 단순화를 위해 ϕᵢ을 사용합니다. 따라서 이 방정식에서 i는 i번째 특징(Xᵢ)을 나타냅니다. 이전 방정식을 단순화하면 다음을 얻을 수 있습니다.
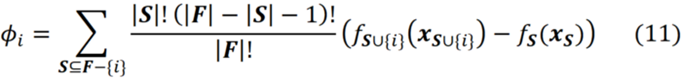
여기서 fₛ(xₛ)는 연합 S에 존재하는 기능에 대한 f의 한계 값이고, f_S∪{i}(x_S∪{i})는 연합 S에 존재하는 기능에 대한 f의 한계 값과 기능 { 나}. Shapley 값의 효율성 속성(공식 5)을 사용하면 다음과 같이 작성할 수 있습니다.
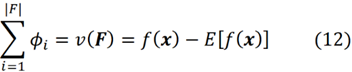
즉, 모든 기능의 Shapely 값의 합은 기능의 현재 값을 사용한 모델의 예측과 모든 교육 예제에 대한 모델의 평균 예측 간의 차이를 나타냅니다.
'Data Analysis' 카테고리의 다른 글
| [ML] SHAP Plots 샘플 (0) | 2023.01.15 |
|---|---|
| [ML] SHAP의 수학적 설명 (0) | 2023.01.14 |
| [ML] SHAP 소개 (3) | 2023.01.13 |
| [통계] 통계 기초 (0) | 2023.01.12 |
| 다중공선성이란? 제거하는 방법은? (0) | 2023.01.11 |




댓글