SHAP 값을 논의하기 전에 SHAP와 같은 설명자 모델에 대한 수학적 설명이 필요합니다. f를 설명할 원래 모델로 정의하고 다음과 같이 정의합니다.

따라서 모델은 특징 벡터 x를 취하고 f(x)는 해당 특징 벡터에 대한 모델 예측입니다. 이 특징 벡터는 훈련 데이터 세트(x⁽ʲ⁾)의 인스턴스 중 하나이거나 훈련 데이터 세트에 존재하지 않는 테스트 특징 벡터일 수 있습니다. 이제 기능 벡터의 기능이 있는지 여부를 표시하기 위해 단순화된 입력 기능 세트를 만듭니다.

벡터 x'를 단순화된 특징 벡터라고 합니다. 각 x'ᵢ은 해당 기능 Xᵢ이 기능 벡터에서 관찰되는지(x'ᵢ =1) 또는 알 수 없는지(x'ᵢ = 0)를 나타내는 이진 변수입니다. 예를 들어, 특징 벡터가
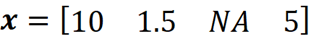

x'를 x에 매핑하는 매핑 함수가 있다고 가정할 수 있습니다.
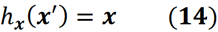
따라서 단순화된 특징 벡터 x'를 사용하여 특징 벡터 x를 반환합니다.
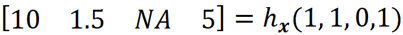
설명자는 M 이진 변수를 사용하는 해석 가능한 모델 g입니다.

여기서 M은 방정식 13에서 단순화된 입력 기능의 수입니다. 행 벡터 z'는 사용 가능한 x 값의 연합을 나타냅니다. 따라서 x'의 0개 요소는 z'에서 항상 0이고 x'의 1개 요소는 z'에서 1 또는 0이 될 수 있습니다. 우리는 z'를 연합 벡터라고 부릅니다. 예를 들어 기능 값이 다음과 같은 경우:

Then the feature vector is:

And the simplified feature is:

Now a value of z’ such as
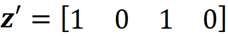
이 두 기능만 z'에 해당하는 1을 가지므로 간단히 연합 S={X₁, X₃}를 나타냅니다. 또한 x'는 대연합 F={X₁, X₂, X₃}를 나타내므로 x'도 연합 벡터로 간주할 수 있다고 결론을 내릴 수 있습니다. 앞에서 언급했듯이 설명자 모델의 예측이 단일 특징 벡터에 대한 원래 모델의 예측에 가깝기를 원합니다. 대연합 x'에 매우 가까운 연합 벡터 z'로 시작한다고 가정합니다. 이 연합에 대한 g의 예측은 단순히 g(z')입니다. 그러나 z'를 사용하여 f의 예측을 어떻게 얻을 수 있습니까? 문제는 f가 연합 벡터가 아닌 특징 벡터를 취한다는 것입니다. 따라서 z'에 해당하는 특성 값을 찾으려면 매핑 함수 hx가 필요합니다. 여기서 hₓ(z')는 z'에 있는 기능의 해당 값을 반환하고 다른 기능의 값은 NA가 됩니다. 예를 들어


z'에 있는 기능에 대한 f의 예측은 다음과 같습니다.

또한 fₓ를 z'에 있는 기능에 대한 f의 한계 값으로 정의합니다. 따라서 다음과 같이 작성할 수 있습니다.

수식 8에서 fₛ는 연합 S에 있는 기능에 대한 f의 한계 값을 나타냅니다. 그러나 여기서는 연합 대신 z'에 초점을 맞추고 fₓ는 z'에 있는 기능에 대한 f의 한계 값을 나타냅니다. . 이 예에서 z'는 연합 S={x₁, x₃}를 나타냅니다. 따라서 다음과 같이 작성할 수도 있습니다.

f(z)인 f의 예측이 (g(z'))인 g의 예측에 매우 근접하여 g가 f가 예측을 위해 사용하는 동일한 프로세스를 모방하도록 합니다. 요약하면, 우리는 원한다.

g가 f를 설명할 수 있다고 주장할 수 있습니다.
g를 기준으로 설명 방법을 분류할 수 있습니다. 추가 기능 속성 방법에는 이진 변수의 선형 함수인 설명자 모델이 있습니다.
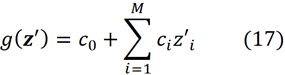
여기서 ci는 일부 상수입니다. 나중에 볼 수 있듯이 SHAP는 이 메서드 클래스에 속합니다. 그래서 방정식 11을 z'로 표현하고자 합니다. x를 특징 벡터로 하고 x'를 단순화된 특징 벡터라고 합니다. Shapley 값이 다음과 같이 표현될 수 있음을 보여줄 수 있습니다.

여기서 ϕᵢ(f, x)는 Shapley 값이 f와 x의 함수임을 강조합니다. 여기서 우리는 x'의 모든 가능한 연합 벡터(x의 모든 연합에 해당)를 고려합니다. 각 연합 벡터 z'에 대해 기능 i의 기여도를 계산합니다. |z'| z'의 0이 아닌 항목 수(해당 연합의 크기) 및 |x'| 는 x'(대연정의 크기)에서 0이 아닌 항목의 수입니다. z'\i는 해당 연합에 {i} 기능이 포함되어 있지 않음을 의미합니다. 따라서 z'\i는 z'의 i번째 요소를 0(z'ᵢ=0)으로 설정한 연합 벡터를 나타냅니다. 예를 들어, 3이 세 번째 특성 x₃를 나타내는 경우 다음과 같이 작성할 수 있습니다.

'Data Analysis' 카테고리의 다른 글
| 설명가능한 인공지능(XAI) 관련 설명(1) (0) | 2023.01.15 |
|---|---|
| [ML] SHAP Plots 샘플 (0) | 2023.01.15 |
| [ML] Shapley Value의 머신러닝 적용 (0) | 2023.01.13 |
| [ML] SHAP 소개 (3) | 2023.01.13 |
| [통계] 통계 기초 (0) | 2023.01.12 |



댓글