•확률 및 확률분포의 개념
1)확률이란 무엇인가?
-우리가 관심을 갖는 경우의 수가 나올 가능성
①수학적 확률: 하나의 주사위(표본공간)를 던져서 5(사건)가 나올 가능성
-이때, 표본 공간의 모든 사건이 동등하게 일어날 수 있음. 즉, 두 사건이 동시에 일어날 수 없음(e.g. 주사위 5와 6이 동시에 발생할 수 없음)
②통계적 확률: 전체 시행 횟수 중 특정 사건이 일어날 횟수의 비율
-n번의 시행횟수에서 어떤 사건이 일어날 횟수를 r이라고 하면 그 사건이 일어난 비율은 r/n
-e.g. 동전을 던졌을 때 4번 던진다고 무조건 앞 2번, 뒤 2번이 나오는 것은 아님
-시행횟수 n이 무한대로 늘어나면 어떤 극한 값에 한 없이 가까워짐
2) 확률분포란 무엇인가?
-어떤 사건이 나타날 가능성인 확률의 분포를 말하는 것
-분포란? 총합이 1인 확률이 각각의 경우에 어떻게 흩어져 있는지 나타낸 것(e.g. 주사위의 경우 각각의 눈이 나올 확률이 각각 1/6씩 분포 되어 있음)

(1)이산확률분포
-확률변수가 가질 수 있는 값이 서로 떨어져 분포되어 있음(e.g. 주사위, 성공/실패 등)
①베르누이 분포
-사건의 결과가 상호배반적인 두 가지 경우만을 갖는 경우. 즉, 성공/실패, 합격/불합격, 동전의 앞/뒷면)
②이항분포
-사건이 n번 시행될 때, 이전 사건이 다음 사건에 영향을 주지 않고 독립적으로 시행
-이항분포에서 n=1일 때, 베르누이 분포라고 함
③포아송분포
-주어진 시간과 공간 범위에서 발생확률이 아주 낮은 사건들의 발생에 관한 이산 확률분포
-즉, 교통사고 발생 건수, 시간당 점포 방문객 수 등
(2) 연속확률분포
-확률변수가 가질 수 있는 값이 서로 이어져 분포되어 있음(e.g. 키, 몸무게 등)
-연속확률변수는 주사위 눈과 같은 방식으로 확률을 할당할 수 없으므로 구간을 설정해 확률을 할당
-
①균등분포
-어떤 구간에서 모든 값이 발견될 가능성이 동일한 분포. 현실적이지 않음
②지수분포
-보통 다음 사건이 일어날 때까지 걸리는 시간이나 간격 등의 분포
③정규분포
-연속확률분포 중 가장 대표적인 분포로 평균을 중심으로 좌우 완전 대칭을 이루는 종형분포를 이름
-가우스분포라고도 불리며, 산술평균, 중위수, 최빈치가 모두 동일하고 정규곡선과 x축이 이루는 면적이 1
-평균과 표준편차*에 의해 결정되는 분포로, 즉 중심극한정리**에 의해 독립적인 확률변수의 평균의 분포를 의미
* 표준편차: 각각의 변량이 평균으로부터 얼마나 떨어져 있는가를 측정하는 지표
** 중심극한정리: 동일분포를 가지는 분포의 평균은 개수가 많아지면 언제나
정규분포로 수렴
-다양한 사회, 자연 현상의 특성을 갖고 있으므로 현실을 단순화 할 수 있도록 도와줌
-George E. P Box “모든 (확률) 모형은 틀렸다. 하지만 그중 어떤 것은 유용하다.”
③’ 표준정규분포
-특성이 이질적인 두 변수의 분포는 서로 비교하기 어려우므로 변수를 표준화(standardization)
-즉, 평균 μ, 표준편차 σ인 확률변수를 평균 0, 표준편차 1인 표준척도로 변환시킨 분포를 이룸
• 정규분포 그래프
-표본 평균 분포 모양이 정규분포 모양이라면 평균값을 중심으로 2 x 표준편차의 범위가 약 95%의 면적을 차지하게 됨
-표본 평균이 존재할 범위를 95%의 신뢰수준으로 산출

• 정규분포를 이룰 경우 평균과 표준편차 값에 따른 확률면적

•정규분포 예제
A 타이어 회사에서 새로 개발한 타이어의 주행 테스트를 시행하였다. 기술자들은 그 타이어의 주행거리를 평균(μ) 36,500km, 그리고 표준편차(σ)를 5,000km로 추정했다. 또한 수집한 자료에 따라 타이어의 주행거리가 정규확률분포를 이룬다고 가정하였다.
a) 몇 퍼센트의 타이어가 4만 km 이상 주행가능하다고 예상할 수 있을까?
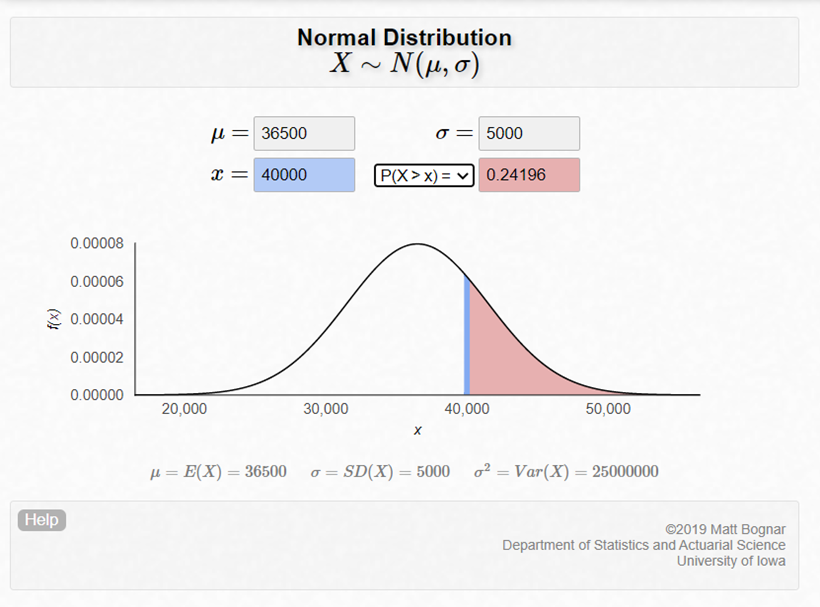
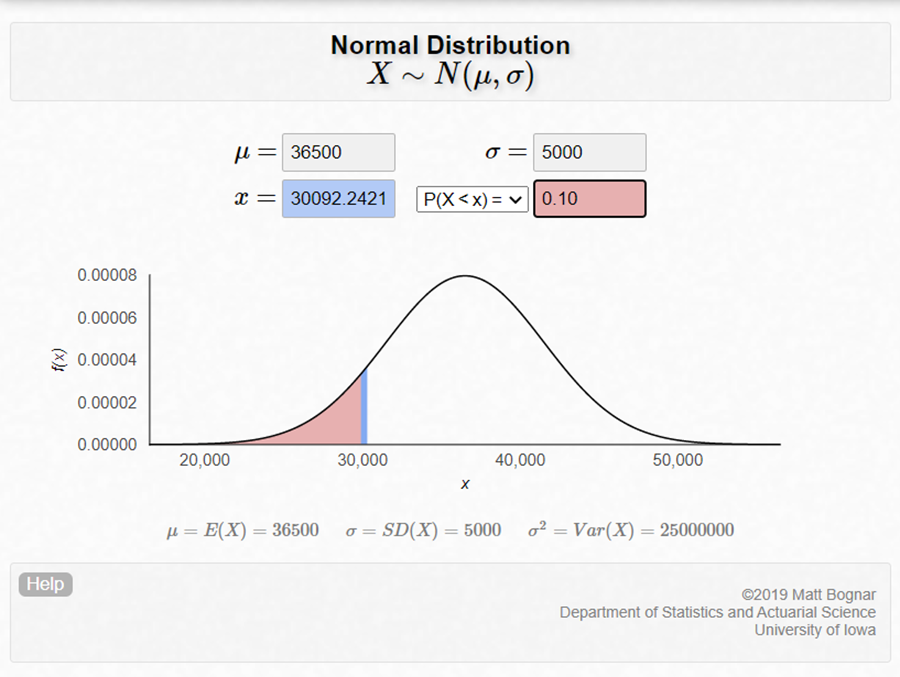
b) A 사는 보증 주행거리에 못 미친 타이어를 교체할 교체 타이어를 할인해 주는 보상 제도를 검토하고 있다. A사가 할인 보상을 받는 타이어의 비율이 10% 이하이길 바란다면, 보증 주행거리를 얼마로 설정해야 할까?
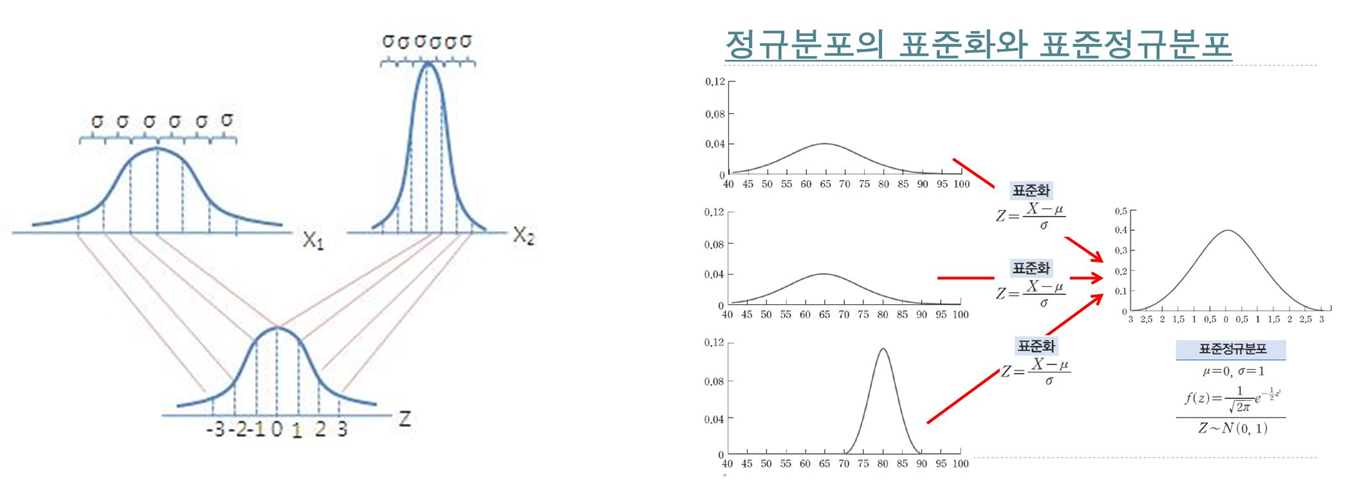
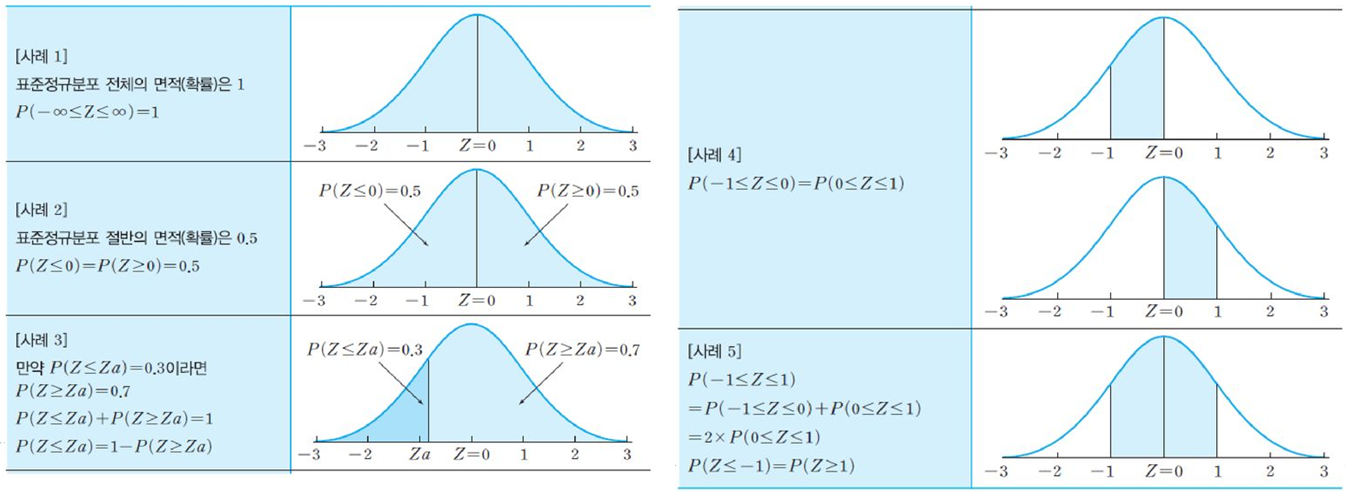
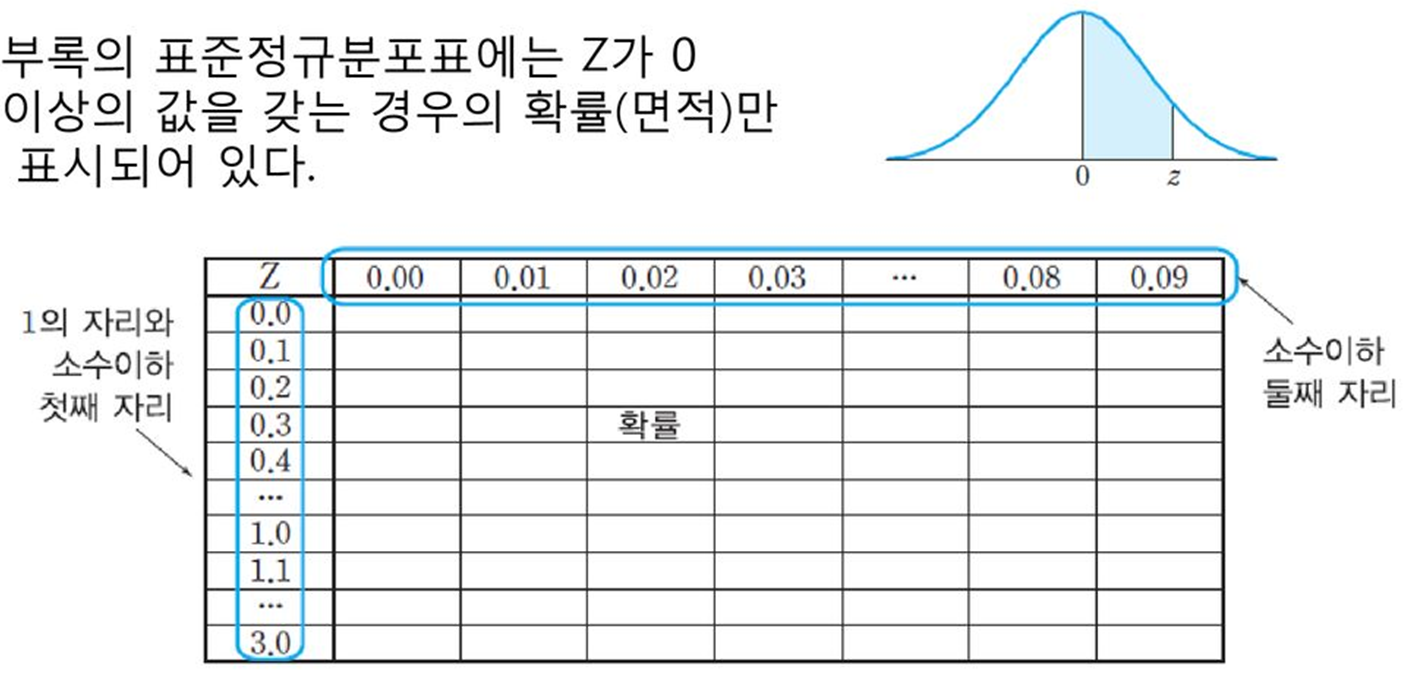
•표준정규분포(standard normal curve)
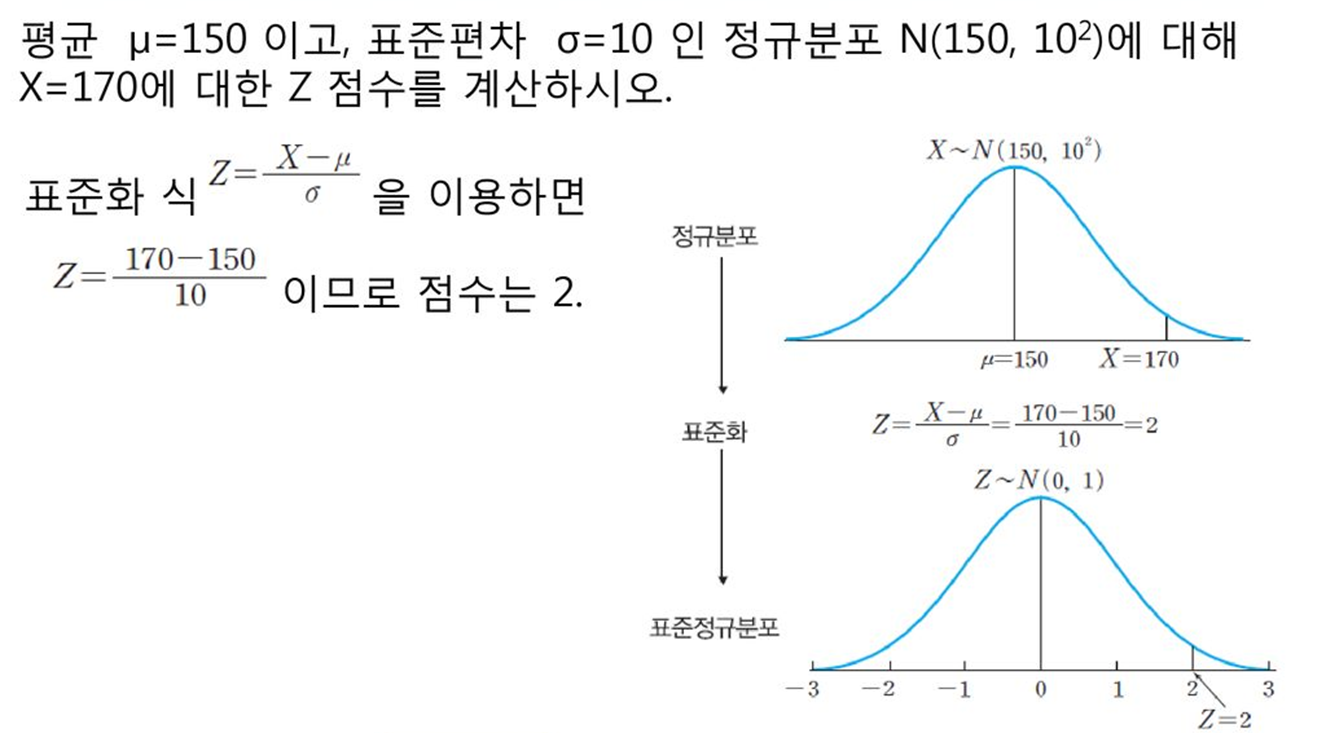
-평균이 μ이고, 표준편차가, σ인 확률변수 X_i를 평균이 0, 표준편차가 1인 표준척도로 변환시킨 분포로 Z분포라고 부름
-Z분포는 정규분포의 특성을 지니고 있으며, 다만 각기 변량들이 평균치로부터 어느 정도 떨어져 있는가를 알기 위해 각각의 변량을 표준화 한 것

•t 분포
-표본의 크기가 작은 소규모 표본 집단을 대상으로 하는 경우에는 Z분포가 아니라 t 분포를 이용해야 한다(표본크기 30 미만일 경우).
-t분포와 정규분포의 가장 큰 차이점은 t분포는 표본 크기에 따라 유형이 달라진다는 점. 즉, 표본 크기가 작을수록 종형에 가까워 정규분포와 차이가 커지지만 표본의 크기가 커지면 정규분포와 유사하게 됨
-예를 들어, n=11일 때, P=0.95의 값은 ±2.23, P=0.99일 때, ±3.17로 Z 값 각각 ±1.96, ±2.56과 차이 발생

'Data Analysis' 카테고리의 다른 글
| [통계] 회귀분석 (1) | 2023.01.21 |
|---|---|
| [기초통계] 추정, 신뢰도 및 가설검정 (1) | 2023.01.20 |
| Urban-GAN(2) (0) | 2023.01.19 |
| Urban-GAN(1) (0) | 2023.01.18 |
| 설명가능한 인공지능(XAI) 관련 설명(5) (1) | 2023.01.18 |




댓글