• 회귀의 의미
1) 회귀의 사전적 의미? Go back to an earlier and worse condition
2 )Francis Galton(1822~1911)의 연구에서 기원
- 부모의 키와 자녀의 키 사이의 관계를 연구해보니 평균으로 돌아가려는 경향을 발견
- 자녀의 키에 영향을 미치는 부모의 키의 영향력 도출

• 회귀분석의 종류

• 회귀분석 적용 사례
- 설명변수가 종속변수에 어떠한 영향을 미치고 있는가?
1) 주택가격 모형(hedonic price model)
hprice=f(주택모형, 입지특성, 공동체/지역 특성)
2) 교통 수요 모형(통행 발생량)
수요량=f(인구, 소득, 자동차 보유율, 밀도 등)
3) 제품생산 비용에 대한 연구
비용=f(설계, 생산, 유통 비용)
4) 개인의 상품 수요
수요=f(제품가격, 타제품 가격, 수입)
5) 지역의 인구 예측
pop=f(고용기회, 인종, 세금, 공공서비스, 접근성 등)
• 종속변수와 설명(독립) 변수
- 회귀분석은 설명변수가 종속변수에 어떠한 영향을 미치고 있는가를 분석하는 통계 방법
- 종속변수(dependent variable): 다른 변수에 영향을 받는 변수
- 독립변수(independent variable) or 설명변수(explanatory variable): 다른 변수에 영향을 주는 변수
• 상관관계
- 종속변수와 설명변수는 서로 상관이 있어야 한다. à 모수에 대한 선형성 가정
- 설명변수는 서로 상관관계가 높으면 안 된다. à 설명변수의 독립성 가정

• 기본 개념
1) 자연 및 사회 현상에서 나타나는 현상의 인과관계를 수학적 근거에 의해 포착
2) 변수 간의 상호작용을 수학적 식으로 나타내어 표기


• 회귀모델의 설정
- 어떤 회귀선이 종속변수를 가장 잘 설명하는가?
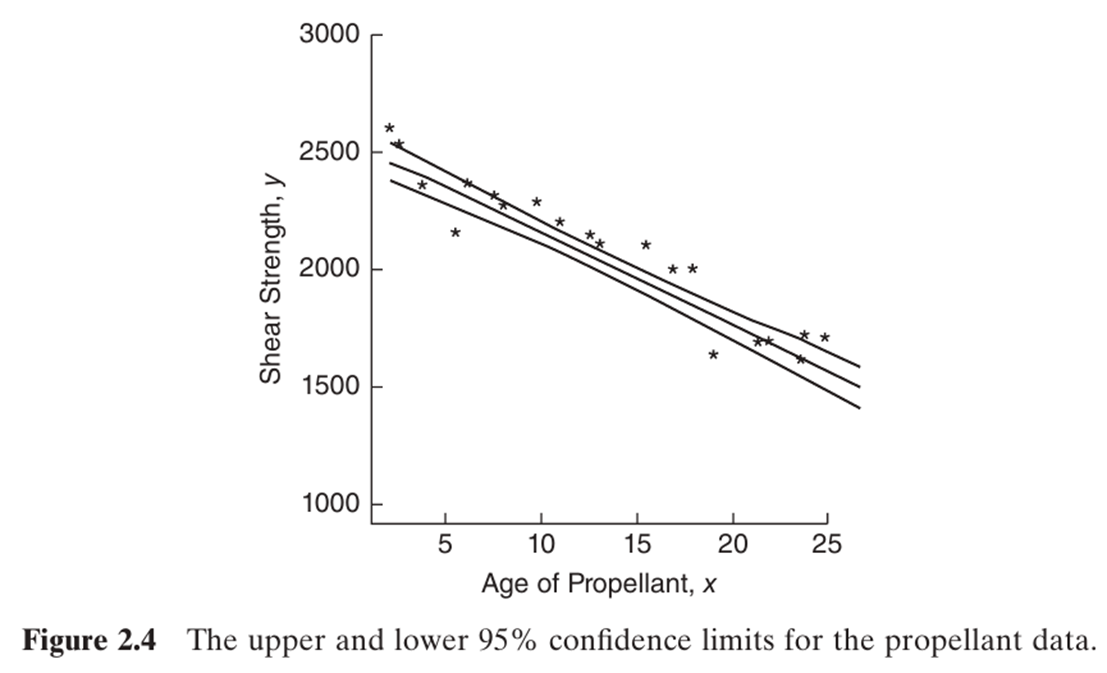
- 어떤 회귀선이 종속변수를 가장 잘 설명하는가? 에러가 가장 작은 회귀선!
--> 최소제곱법(Least Square Method)
--> 가장 기본적인 회귀분석 Ordinary least squares (OLS)
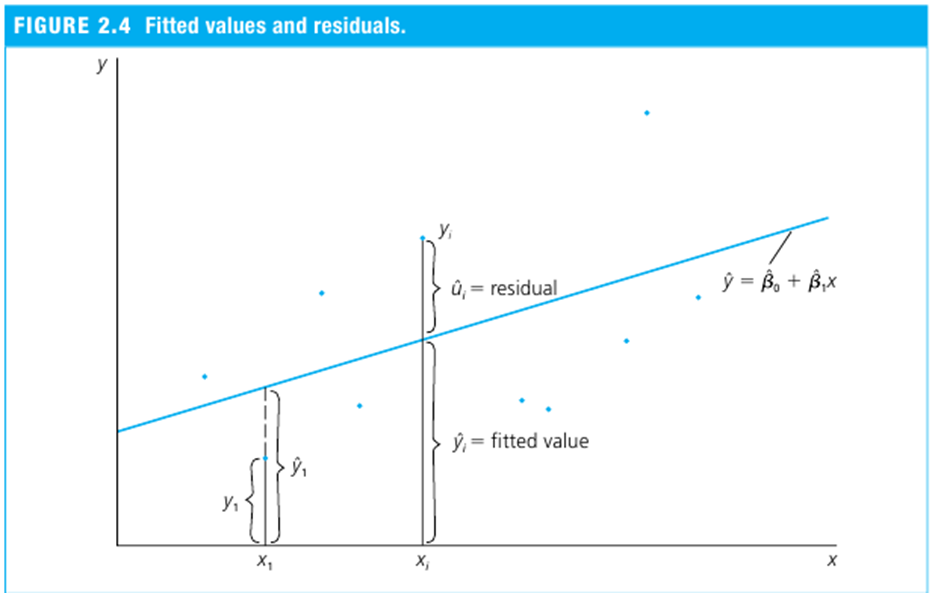
• 오차항(error term)
- 실제 현상에서 y=Xβ 와 같이 완벽한 관계는 나타날 수 없다.
- 왜냐하면, 측정에 오류가 발생할 수 있고(measurement error), 종속변수를 설명하는 정보가 불충분할 수 있기 때문에(incomplete or imperfect information)
- 따라서 회귀식에는 아래와 같이 error 가 포함되며, 오차항이 모든 통계적 분석에서 가장 중요한 요소이다.
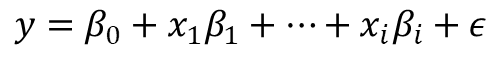
• 최소제곱법
-어떤 회귀선이 종속변수를 가장 잘 설명하는가? 에러가 가장 작은 회귀선!
-잔차의 합을 최소화하는 추정량을 의미
y=xβ+ε,
ε =y-xβ
ε′ε=(y-xβ)′(y-xβ)=(y′-β′x′)(y-xβ)=y′y-y′xβ-β′x′y+β′x′xβ
∂/∂β ε′ε=0=-y′x-x′y+2x′xβ=-x′y-x′y+2x′xβ
x′xβ=x′y
β=(x′x)^(-1) x′y (Q=(x′x)^(-1) x′)
β=Qy
• 회귀모델의 설정
- 반복적인 과정을 수행하여 회귀모델을 설정
1) 실제 세계에서 관심을 가진 현상의 이론이나 가설을 수립
2) 데이터 수집
3) 모델 설정 및 추정
4) 통계 분석을 통해 모델의 적합성과 타당성 검정
5) 문제가 있을 경우 다시 반복

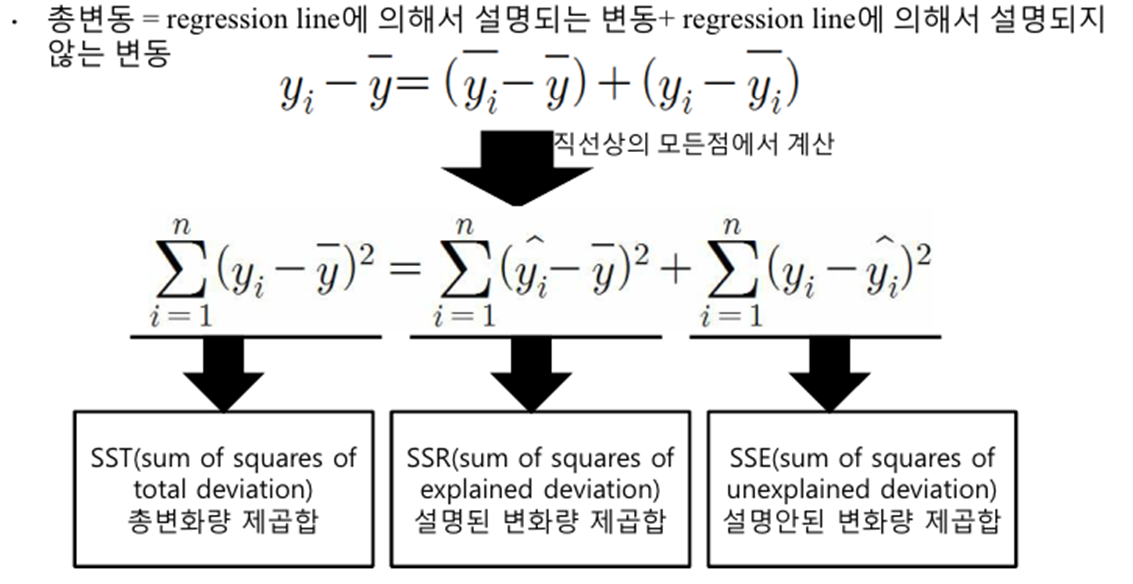
• 적합도 검정(goodness-of-fit test)
- 적합도 검정은 계수를 구해 도출한 회귀식이 표본의 실제값을 얼마나 잘 설명하는지를 확인하는 방법
- 추정된 회귀식의 설명력에 대한 척도를 R2(회귀선의 설명력, 결정계수)으로 표현
- 보통 0부터 1사이의 숫자로 나타낸다. 0에 가까울수록 작은 설명력을, 1에 가까울수록 큰 설명력
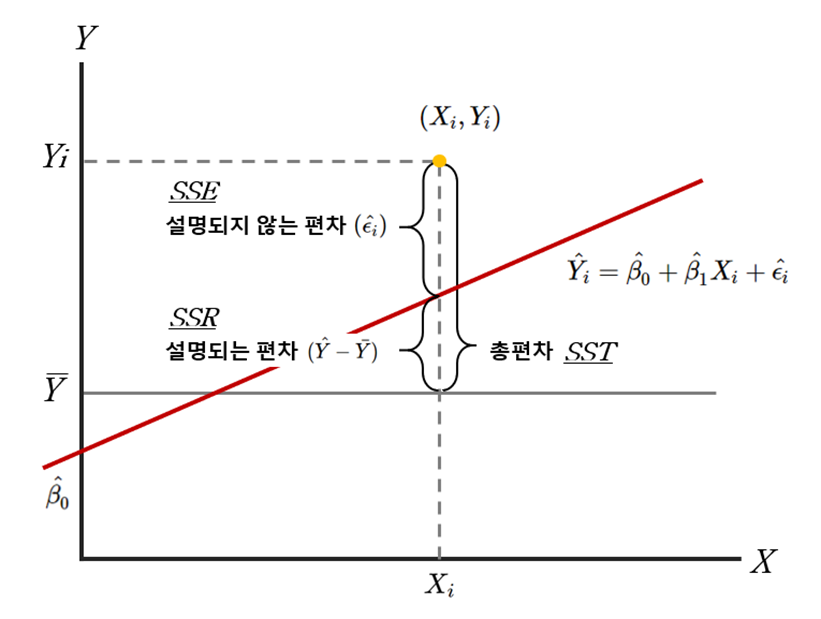
1) 결정계수

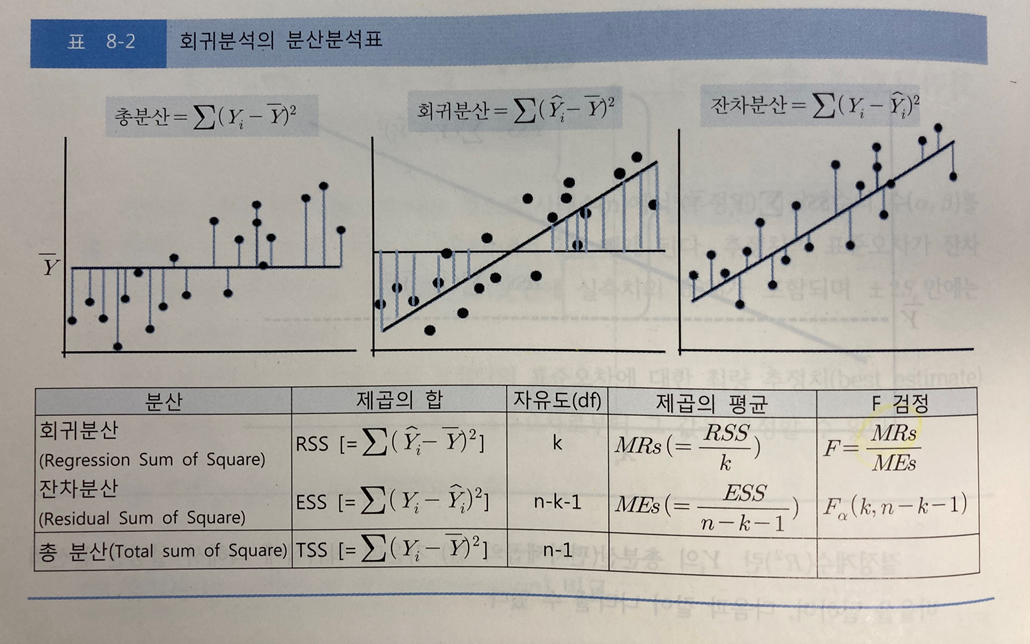
2) F 검정
- 회귀식에 의해 설명된 회귀분산과 회귀식에 의해 설명되지 못한 잔차의 비율을 비교
- F 값이 커질수록 설명력이 높은 회귀식
- 계산된 F값은 평균분산의 비율
• 유의성 검정
- 회귀분석에서는 두 모집단, 즉 설명변수(x1, x2, x3, … , xi)에 상응하는 종속변수(y1, y2, y3, … , yi)에 대해 Y_i=α+βX_i의 회귀식이 성립된다고 가정한다. 여기에서 회귀모델의 알려져 있지 않은 모수(parameter)인 α, β, σ^2값을 추정하기 위해 표본으로부터 수집된 데이터를 통해 최소자승법에 의해 모수를 추정하는 것(Y ̂=a+bX_i)
1) 모수 β에 대한 검정
- 표본에서 추정된 회귀계수 b에 대한 통계적 유의성을 검정하기 위해 모수 β에 대한 귀무가설과 그에 대립되는 연구 가설 수립
- 연구가설: X변수와 Y변수 간에 직선적인 관계가 있다
- 귀무가설: 두 변수 사이에는 아무런 관계가 없다.
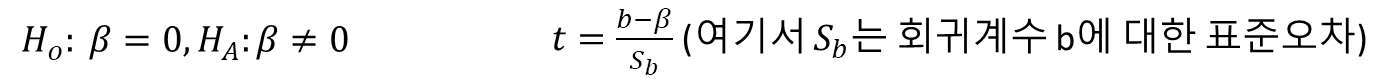
- 추정치의 표준오차가 알려져 있는 경우에는 다음과 같다.
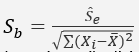
- 귀무가설에서는 β=0을 전제하므로 t검정은 다음과 같이 나타낼 수 있으며, β에 대한 검정은 자유도 n-2와 유의수준 α에서의 t임계치와 t_c 값을 비교하여 귀무가설을 기각 또는 수용한다.
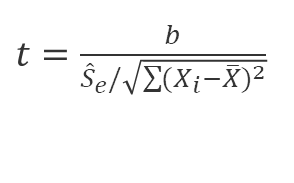
- 한편 n-2의 자유도와 표준오차 S_b, t분포를 하고 있는 회귀계수 b로부터 β의 신뢰구간음 다음과 같다.
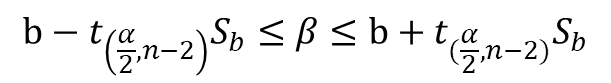
2) 특정한 X_o에 대한 예측치 Y ̂ 에 대한 구간 추정
- 회귀분석을 수행할 경우 표본 데이터에 포함되지 않은 〖X의 변량 X〗_o에 대응하는 예측치 Y ̂_o값으로부터 모수 Y_o 를 추정하는 경우가 발생
- 추정된 회귀식에서 X_o일 때의 예측된 Y ̂_o값은 모수 Y_o와 차이가 있을 수 있다. 왜냐면 추정된 회귀식 Y ̂=a+bX_i에서 a,b는 단지 모수 α, β의 추정치이므로 모수와 차이가 있을 수 있기 때문
- 특히 회귀계수 β값도 표준오차에 따라 상당히 넓은 구간의 오차를 가질 수 있으며 이를 표준오차(standard error of prediction)이라고 한다.
- 주어진 X_o값에 대응하는 예측치 Y ̂_o의 표준오차는 다음과 같다.
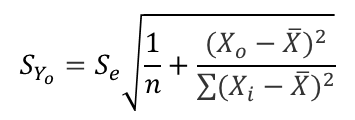
- 주어진 X_o값에 대응하는 예측치 Y ̂_o의 표준오차는 표본의 크기가 클수록 작아지며, X_o가 평균으로부터 멀리 떨어져 있을수록 표준오차가 커짐
- 표본의 크기가 작은 소규모 표본일 때 X_o에 대응하는 Y ̂_o의 신뢰구간은 t분포를 사용하며, 표본의 크기가 클 경우 Z분포를 이용한다.
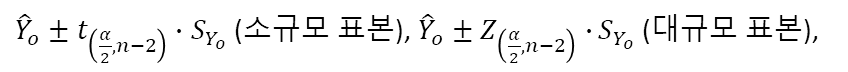
- 일례로 X_o 값에 대응하는 Y ̂_o의 95% 구간 범위는 다음과 같다.
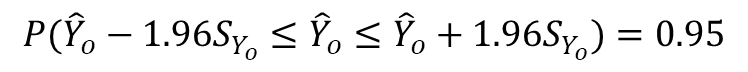
• 더미변수
- 더미(dummy)는 회귀분석에서 사용되는 범주형 설명변수
- 예를 들면,
1) 성별(남,녀)
2) 인종(백인,흑인)
3) 혼인상태(미혼,기혼)
4) 질병발생여부(감염, 비감염)
- 범주는 이원화(dichotomized)(0, 1) 혹은 3개 이상(0, 1, 2)
1) 성별(남, 여) 0: 남, 1: 여
2) 인종(백인, 흑인) 0: 흑인, 1: 백인
3) 혼인상태(미혼,기혼) 0: 미혼, 1: 기혼
4) 질병발생여부(감염, 비감염) 0: 미혼, 1: 기혼
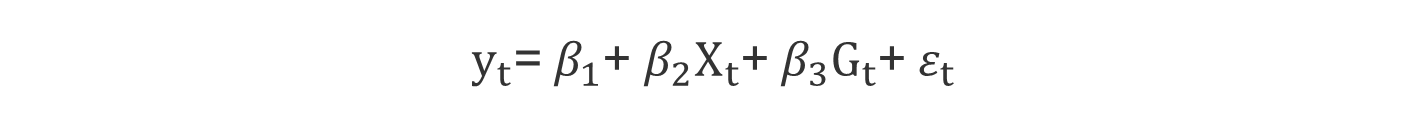
- For male: G_t=1
- For female: G_t=0 (참조집단, reference group)
- y_t = wage rate per hour
- X_t = years of experience
• 초임에 있어 여성 노동자들에 대한 차별여부 검정
H0: β3=0, H1: β3>0
• 초임에 있어 여성과 남성 간에 차이가 있는 가를 검정
H0: β3=0, H1: β3≠0
• 절편 더미변수
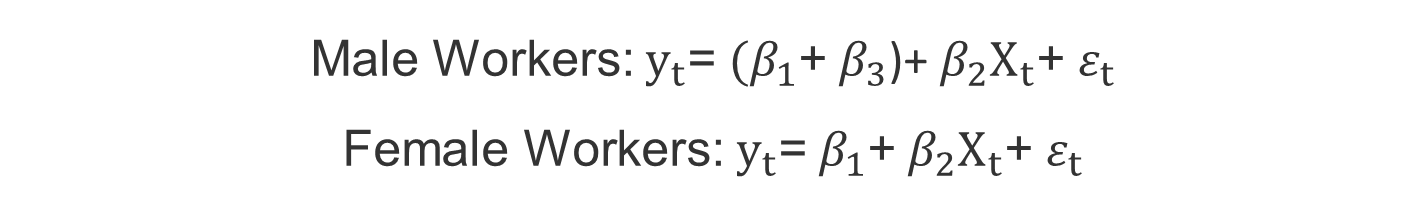
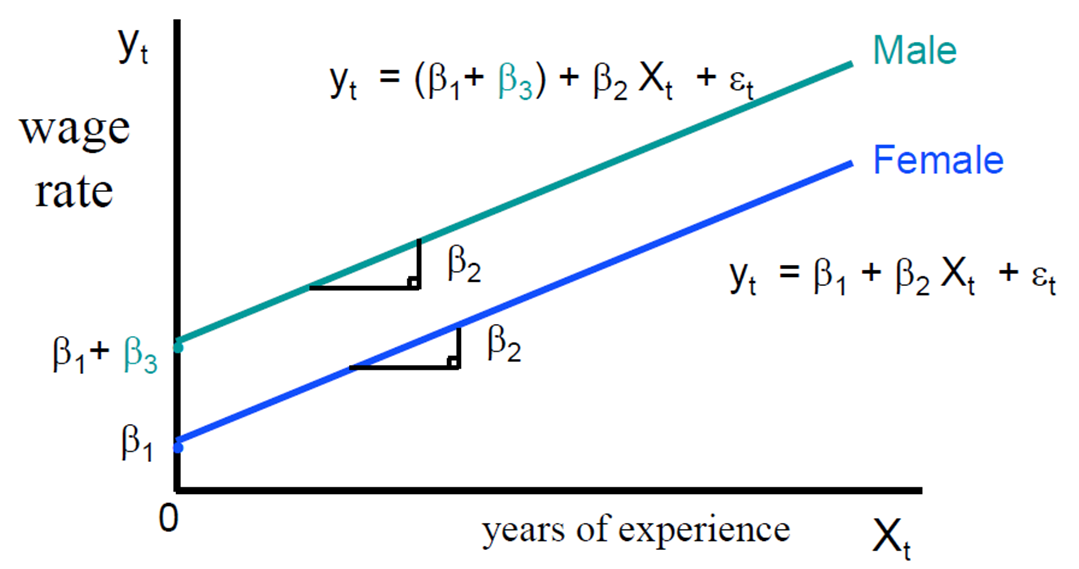
• 기울기 더미변수
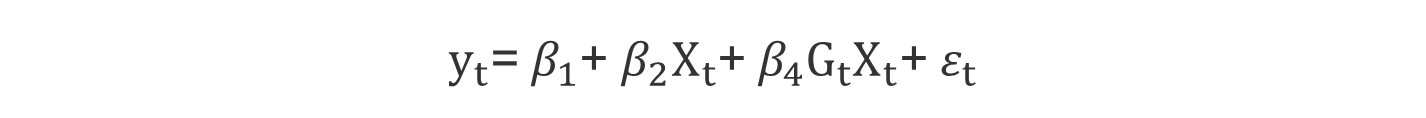
- For male: Gt=1
- For female: Gt=0
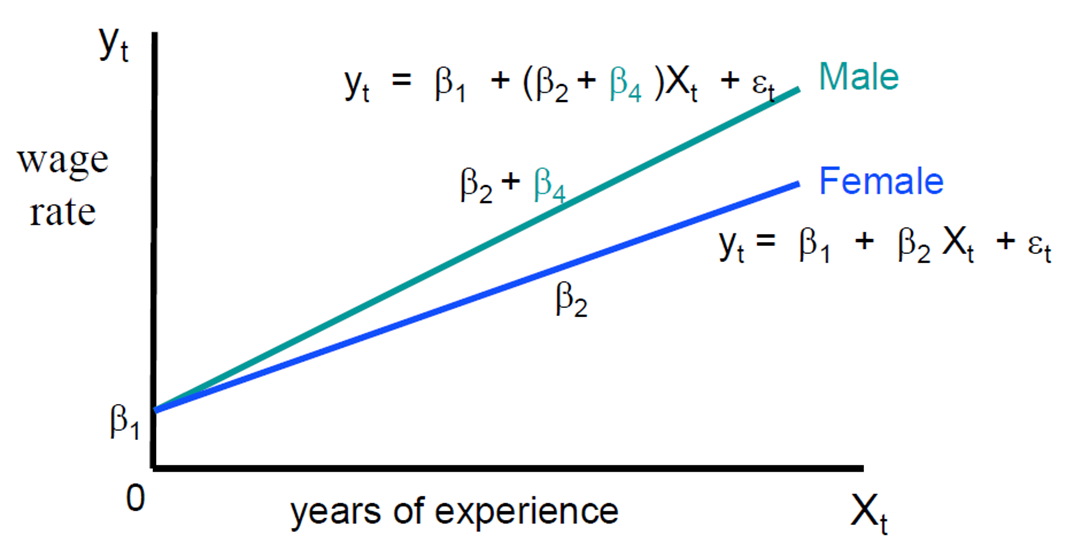
• 남성 여성 모두 동일한 초임 β1을 갖지만 그들의 경력에 따른 임금율은 다른 비율로 증가(차이= β4)
- Male: yt= β1+ β2 Xt+ β4 Xt+ εt
- Female: yt= β1+ β2 Xt+ εt
• β4>0은 남성의 임금율이 여성에 비해 빠르게 증가함을 의미
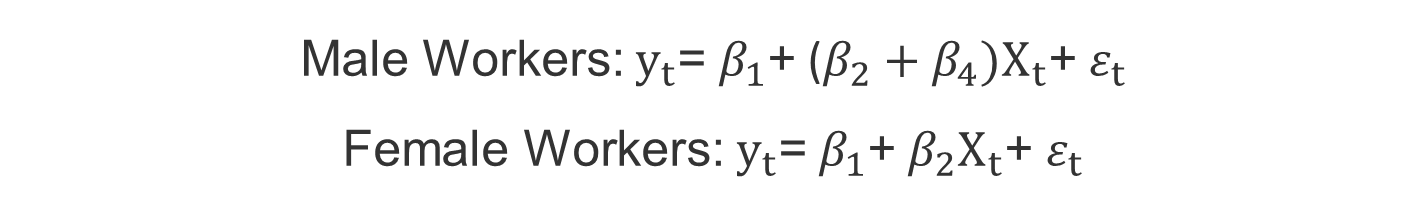
• 상호작용
- 둘 혹은 그 이상의 더미변수를 도입하는 경우, 그들 간의 상호작용도 필요할 수 있음
예)
성별) For female: G_t=0, For male: G_t=1
인종) For non-white: R_t=0, For white: R_t=1
- 만약 성별과 인종의 상호작용이 없다면: 성별 임금격차는 인종과 상관이 없음
- yt= β1+ β2 Xt+ δ1 Rt+δ2 Gt+ εt
- 만약 성별과 인종의 상호작용이 있다면: 성별 임금격차가 인종에 의존함
- yt= β1 + β2 Xt + δ2 Rt + δ1 Gt + γRt Gt + εt
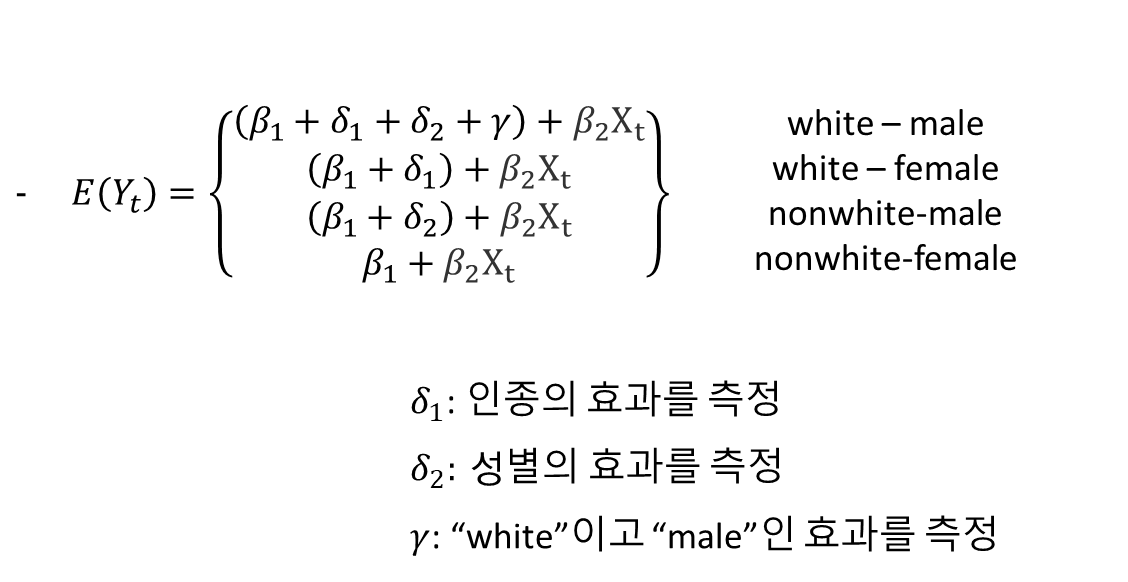
• 다양한 범주를 갖는 더미 변수
- 많은 변수가 두 개 이상의 범주를 가짐
예) 교육 수준(고졸, 대졸, 대학원 졸 이상)
- 각 범주를 개별적인 더미 변수로 만들 수 있음
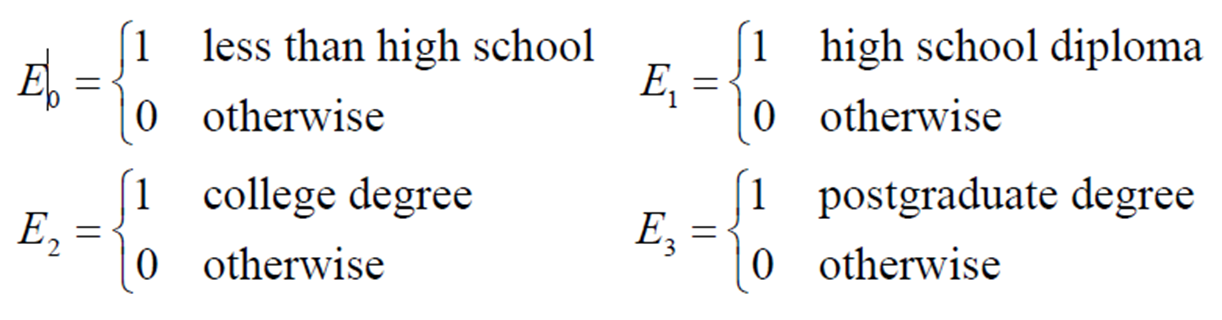
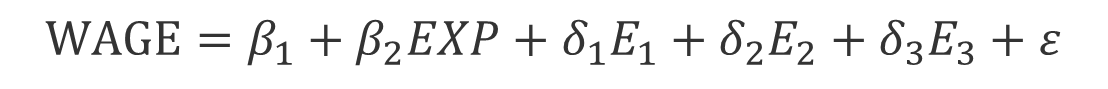

• 더미 변수들의 모수들은 참조집단(여기서는 고졸 미만 집단) 대비 기대되는 임금 격차를 나타냄
'Data Analysis' 카테고리의 다른 글
| [통계] 이산선택모형 (0) | 2023.01.25 |
|---|---|
| 다중 변수 시계열 분석(Temporal Fusion Transformers) (0) | 2023.01.21 |
| [기초통계] 추정, 신뢰도 및 가설검정 (1) | 2023.01.20 |
| [통계] 확률과 확률분포 (0) | 2023.01.19 |
| Urban-GAN(2) (0) | 2023.01.19 |




댓글