•추정이란?
-모집단은 크기가 너무 크기 때문에 전수조사를 하기 위해서는 엄청난 비용과 시간이 소요되며, 경우에 따라서는 전수조사가 불가능
-대부분의 경우 모집단을 대표할 수 있는 표본을 추출하여 그 표본의 통계량으로 모집단의 모수 추정
-
•사례
-A대학교 학생의 평균 키를 추정하고자 할 경우 25,000명이 넘는 모집단인 A대학교 학생 전체를 조사하는 것은 어려움
-학생들 중에서 100명을 표본으로 추출하여 구한 평균 키로 모집단인 A대학교 학생 전체의 평균 키를 추정
•신뢰구간: 점추정(point estimation)과 구간추정(interval estimation)
1)점추정은 모수가 얼마일 것이라고 하나의 수치를 추정하는 것. 여기서 모수는 모평균, 모분산, 모표준변차, 모비율 등 모집단의 특성에 관한 수치들을 의미
2)구간추정은 모수가 어느 값 a와 어느 값 b 사이, 즉 어떤 구간 내에 몇 %의 확률로 존재할 것이라고 추정하는 것. 그 확률을 신뢰수준(confidence level) 또는 신뢰도라고 부르고, 그 추정한 구간을 신뢰구간(confidence interval)이라고 부름

•구간추정(interval estimation)
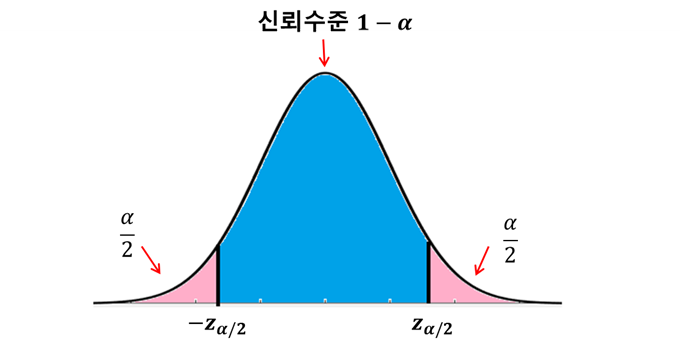
-모수가 신뢰구간 안에 포함되지 않을 확률을 보통 α로 표현
-모수가 신뢰구간 안에 포함될 확률, 즉 신뢰수준은 1−α로 표현
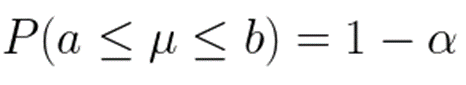
만약 신뢰수준 1−α이 0.95 즉, 95%라면 α=0.05

•구간추정(interval estimation)

•모분산을 알 때 모평균의 신뢰구간 추정

-만약 95%의 신뢰수준으로 모평균이 신뢰구간 내에 존재한다고 하면, 표준정규분포표에 의해 다음과 같이 쓸 수 있다.

•모분산을 알 때 모평균의 신뢰구간 추정
-신뢰수준 1−α1−α인 신뢰구간은 다음과 같이 유도

•모분산을 모를 때 모평균의 신뢰구간 추정
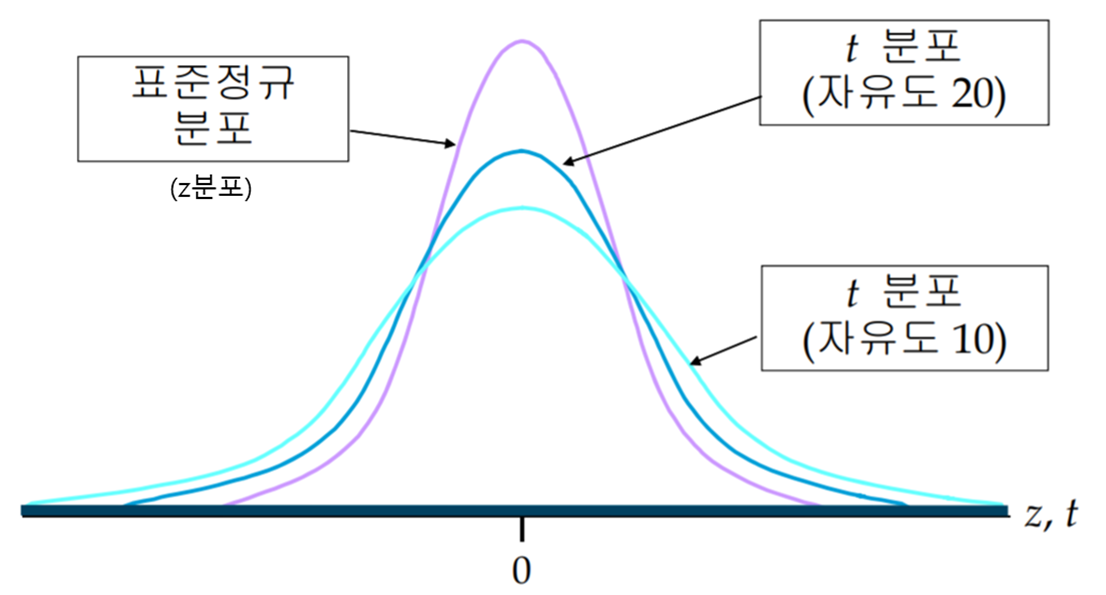
-모분산을 모를 때는 t분포를 사용
-t분포는 정규분포와 상당히 비슷한데 중심부는 낮아지고 양쪽 꼬리는 좀 더 높은 종 형태(아래 그림 참고)
-자유도가 작을수록 꼬리부분이 높아지고, 자유도가 높을수록 표준정규분포에 가까워진다.
-이 자유도는 표본의 크기에 따라 결정(자유도 = n - 1)
•모분산을 모를 때 모평균의 신뢰구간 추정
-모분산, 즉 모표준편차를 모르기 때문에 모표준편차 σ 대신에 표본표준편차 s를 사용
-t통계량은 다음과 같이 쓸 수 있다.
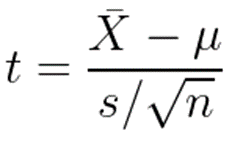

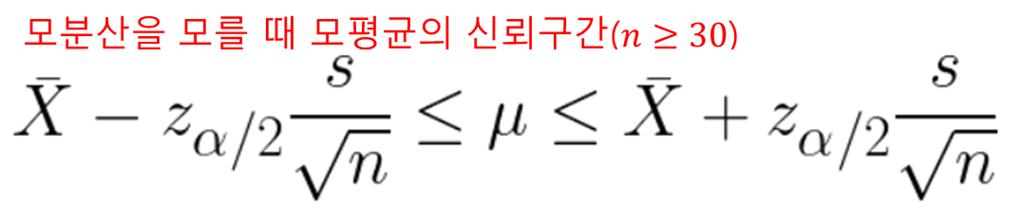
<가설검정>
• 연구자가 추측하여 두 개 이상의 변수들 간의 잠정적인 관계를 나타냄
• 특징 : 연구자가 밝히고자 하는 사항은 선언문 형식으로 표현
• 사계) 광고는 매출액 증대에 긍정적 영향을 미친다.
- 대립가설(Ha) : 연구자가 주장하기 원하는 가설
- 귀무가설(Ho) : 대립가설의 반대내용으로 통계적 검증의 대상이 됨
--> 귀무가설을 기각하고 대립가설을 채택하기 위해 귀무가설의 잘못됨을 입증해야 함
--> 귀무가설 기각: 대립가설 채택
--> 귀무가설 기각하지 않음: 대립가설 기각
• 1종오류 : 귀무가설이 진실임에도 불구하고 기각하는 오류
•2종오류 : 귀무가설이 허위임에도 불구하고 기각하지 않는 오류
•가설(hypothesis)의 정의
-연구자가 모집단이 가지고 있는 어떤 특성(모수)에 관한 가정이나 주장을 실제 검증 이전에 하나의 문장으로 표현한 것. 귀무가설과 대립가설이 있음
•귀무가설(null hypothesis)
-어떤 주장이 잘못되었다는 것이 증명되지 않는 이상이 진실로 수용되는 것
-귀무가설은 집단 간 하나의 검정변수에 대해 평균의 차이가 존재하지 않는다든가, 혹은 두 변수 간 상호관련성이 없다는 등의 내용으로 이루어짐(H_0)
•대립가설(alternative hypothesis)
-연구자가 증명하고자 하는 혹은 채택시키고자 하는 내용으로 표현된 가설
-수집된 자료 분석을 통하여 하나의 객관적인 사실로 받아 들여지기를 바라는 내용으로 구성된 가설(H_1)
-대립가설이 사실이라고 증명이 되면 귀무가설은 기각되지만 그렇지 않은 경우에는 대립 연구 가설이 기각되고 대신 귀무가설이 수용
•가설검정 절차
1단계 : 가설설정
-연구가설 설정 : 입증하고자 하는 내용
-귀무가설 설정 : 입증하고자 하는 내용의 반대
-검증종류 설정 : 양측 or 단측
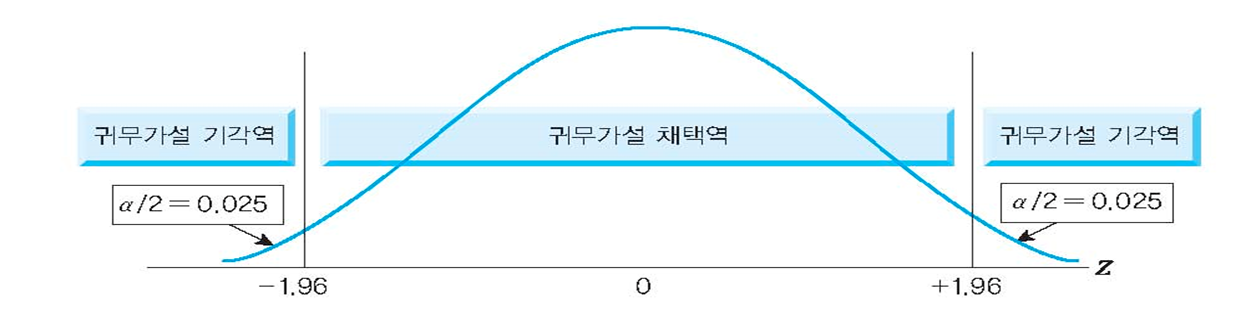
2단계 : 임계치 설정(가장 보편적으로 사용되는 알파값은 0.05(95% 신뢰수준))
-표본의 검증통계량의 값과 비교할 수 있는 기준(신뢰구간의 상,하한값)
-평균에 대한 가설 검증 : T 분포
-분산에 대한 가설 검증 : F 분포
3단계 : 검증통계량 결정
-표본에 따라 단위가 다르므로 이를 표준화시켜 계산한 값
-Z통계량(정규분포) : 단일집단에서 모집단의 분산 알고 표본크기가 큰 경우(N>30)
-T통계량(T분포) : 모집단의 분산 모르고 표본크기가 작은 경우
-F통계량 : 둘 이상 집단의 평균값비교시
-χ2 통계량 : 둘 이상 집단의 특성차이 비교시
4단계 : 가설채택 기준 결정
1) 유의수준(α) 결정
2) 가설검정
(1) 임계치를 이용한 가설검정
- 검정통계량 > 임계치 : 귀무가설 기각, 대립가설 채택
- 검정통계량 < 임계치 : 귀무가설 채택, 대립가설 기각
(2) p-value을 이용한 가설검정
- p-value > α 값 : 귀무가설채택, 대립가설 기각
- p-value < α 값 : 귀무가설 기각, 대립가설 채택
•유의수준(p-value)
•정의: 귀무가설이 진실이나 기각할 확률, 귀무가설을 기각하는 것이 잘못 될 확률, 대립가설을 채택하는 것이 잘못될 확률
-P-value = 0.7 : 귀무가설을 기각하는 것이 잘못될 확률이 0.7
-유의수준이 낮을수록 연구자는 자신있게 대립가설을 주장할 수 있음
-허용오차수준(α) : p-value의 허용수준, α= 0.05가 일반적
-p-value가 작을수록, α 가 클수록 귀무가설 기각 가능성 큼

'Data Analysis' 카테고리의 다른 글
| 다중 변수 시계열 분석(Temporal Fusion Transformers) (0) | 2023.01.21 |
|---|---|
| [통계] 회귀분석 (1) | 2023.01.21 |
| [통계] 확률과 확률분포 (0) | 2023.01.19 |
| Urban-GAN(2) (0) | 2023.01.19 |
| Urban-GAN(1) (0) | 2023.01.18 |




댓글