이 연구에서 소개하는 Temporal Fusion Transformers는 시간 불변하는 변수가 포함된 모형의 시계열 분석 방법으로 2021년에 소개된 Python 패키지이다. 시계열 데이터를 연구하는 많은 분야에서 사용되고 있으며, 앞으로도 더 많은 활용이 기대되는 방법이다. 여기에서는 원문을 해석하여 설명하는 방식으로 방법을 소개하고자 한다. 방법에 대해 더 자세한 내용을 알고 싶은 분은 원문을 참조하기 바란다. 원문은 아래와 같다.
Lim, B., Arık, S. Ö., Loeff, N., & Pfister, T. (2021). Temporal fusion transformers for interpretable multi-horizon time series forecasting. International Journal of Forecasting, 37(4), 1748-1764.
Abstract
다중 수평 예측에는 종종 정적(즉, 시불변) 공변량, 알려진 미래 입력 및 과거에만 관찰되는 기타 외생 시계열을 포함하여 입력이 대상과 상호 작용하는 방식에 대한 사전 정보 없이 복잡한 입력 혼합이 포함됩니다. . 여러 딥 러닝 방법이 제안되었지만 일반적으로 실제 시나리오에 있는 전체 입력 범위를 사용하는 방법을 밝히지 않는 '블랙박스' 모델입니다. 이 백서에서는 고성능 다중 수평선 예측과 시간 역학에 대한 해석 가능한 통찰력을 결합한 새로운 주의 기반 아키텍처인 TFT(Temporal Fusion Transformer)를 소개합니다. 다양한 규모에서 시간적 관계를 학습하기 위해 TFT는 로컬 처리를 위해 순환 계층을 사용하고 장기 종속성을 위해 해석 가능한 자기 주의 계층을 사용합니다. TFT는 특수 구성 요소를 사용하여 관련 기능을 선택하고 일련의 게이팅 레이어를 사용하여 불필요한 구성 요소를 억제하여 광범위한 시나리오에서 고성능을 가능하게 합니다. 다양한 실제 데이터 세트에서 기존 벤치마크에 비해 상당한 성능 향상을 시연하고 TFT의 세 가지 실용적인 해석 가능성 사용 사례를 강조합니다.
Introduction
다중 수평 예측, 즉 여러 미래 시간 단계에서 관심 변수의 예측은 시계열 기계 학습 내에서 중요한 문제입니다. 한 단계 앞선 예측과 달리 다중 수평 예측은 사용자에게 전체 경로에 대한 예측에 대한 액세스를 제공하여 향후 여러 단계에서 작업을 최적화할 수 있도록 합니다(예: 소매업체가 다가오는 시즌 전체에 대해 인벤토리를 최적화하거나 환자를 위한 치료 계획을 최적화하는 임상의). 다중 수평선 예측은 소매(Böse et al., 2017; Courty & Li, 1999), 의료(Lim, Alaa, & van der Schaar, 2018; Zhang & Nawata, 2018) 및 경제성(Capistran, Constandse, & Ramos-Francia, 2010) – 이러한 응용 분야에서 기존 방법에 대한 성능 개선은 매우 중요합니다.
실제 다중 수평선 예측 애플리케이션은 일반적으로 미래에 대한 알려진 정보(예: 다가오는 휴일 날짜), 기타 외생 시계열(예: 과거 고객 발 트래픽)을 포함하여 그림 1과 같이 다양한 데이터 소스에 액세스할 수 있습니다. ) 및 정적 메타데이터(예: 상점 위치) – 상호 작용 방식에 대한 사전 지식 없이. 상호 작용에 대한 정보가 거의 없는 이러한 데이터 소스의 이질성은 다중 수평선 시계열 예측을 특히 어렵게 만듭니다.
심층 신경망(DNN)은 다중 수평선 예측에 점점 더 많이 사용되어 기존 시계열 모델에 비해 강력한 성능 개선을 보여줍니다(Alaa & van der Schaar, 2019; Makridakis, Spiliotis, & Assimakopoulos, 2020; Rangapuram et al., 2018). . 많은 아키텍처가 순환 신경망(RNN) 아키텍처의 변형에 초점을 맞추었지만(Rangapuram et al., 2018; Salinas, Flunkert, Gasthaus, & Januschowski, 2019; Wen et al., 2017) 최근 개선 사항에서도 주의 기반 변압기 기반 모델(Li et al., 2019)을 포함하여 과거의 관련 시간 단계 선택을 향상시키는 방법(Fan et al., 2019). 그러나 이들은 종종 다중 수평선 예측에 일반적으로 존재하는 다양한 유형의 입력을 고려하지 못하고 모든 외생 입력이 미래에 알려져 있다고 가정합니다(Li et al., 2019; Rangapuram et al., 2018; Salinas et al., 2019) – 자기회귀 모델의 일반적인 문제 – 또는 각 단계에서 다른 시간 종속 기능과 단순히 연결되는 중요한 정적 공변량을 무시합니다(Wen et al., 2017). 시계열 모델의 많은 최근 개선 사항은 아키텍처를 고유한 데이터 특성과 정렬한 결과입니다(Koutník, Geff, Gomez, & Schmidhuber, 2014; Neil et al., 2016). 우리는 다중 수평 예측을 위해 적절한 귀납적 편향을 가진 네트워크를 설계함으로써 유사한 성능 이득을 얻을 수 있다고 주장하고 입증합니다.
일반적인 다중 수평선 예측 입력의 이질성을 고려하지 않는 것 외에도 대부분의 최신 아키텍처는 예측이 많은 매개변수 간의 복잡한 비선형 상호 작용에 의해 제어되는 '블랙박스' 모델입니다. 이는 모델이 예측에 도달하는 방법을 설명하기 어렵게 만들고, 결과적으로 사용자가 모델의 출력을 신뢰하고 모델 빌더가 이를 디버그하는 것을 어렵게 만듭니다. 불행히도 DNN에 일반적으로 사용되는 설명 가능성 방법은 시계열에 적용하기에 적합하지 않습니다. 기존 형식에서 사후 방법(예: LIME(Ribeiro et al., 2016) 및 SHAP(Lundberg & Lee, 2017))은 입력 기능의 시간 순서를 고려하지 않습니다. 예를 들어 LIME의 경우 각 데이터 포인트에 대해 대리 모델이 독립적으로 구성되고 SHAP의 경우 인접 시간 단계에 대해 기능이 독립적으로 고려됩니다. 이러한 사후 접근 방식은 시간 단계 간의 종속성이 일반적으로 시계열에서 중요하기 때문에 설명 품질이 좋지 않습니다. 반면에 Transformer 아키텍처(Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, & Polosukhin, 2017 ). 이를 적용하기 위한 기본적인 주의 사항은 다중 수평선 예측에는 언어나 음성과 달리 다양한 유형의 입력 기능이 포함된다는 것입니다. 기존 형식에서 이러한 아키텍처는 다중 수평 예측을 위한 관련 시간 단계에 대한 통찰력을 제공할 수 있지만 주어진 시간 단계에서 다양한 기능의 중요성을 구별할 수는 없습니다. 전반적으로 고성능을 위한 다중 수평 예측에서 데이터의 이질성을 해결하기 위한 새로운 방법의 필요성 외에도 사용 사례의 요구 사항을 감안할 때 이러한 예측을 해석 가능하게 만드는 새로운 방법도 필요합니다.
이 논문에서 우리는 새로운 형태의 해석 가능성을 가능하게 하는 동시에 고성능을 달성하는 다중 수평 예측을 위한 주의 기반 DNN 아키텍처인 TFT(Temporal Fusion Transformer)를 제안합니다. 최첨단 벤치마크에 비해 상당한 성능 향상을 얻기 위해 아키텍처를 다중 수평 예측에 공통적인 잠재적 입력 및 시간 관계의 전체 범위와 정렬하는 여러 참신한 아이디어를 도입합니다. 특히 (1) 정적 공변량을 통합합니다. 네트워크의 다른 부분에서 사용하기 위해 컨텍스트 벡터를 인코딩하는 인코더, (2) 관련 없는 입력의 기여도를 최소화하기 위한 전체 게이팅 메커니즘 및 샘플 종속 변수 선택, (3) 알려지고 관찰된 로컬 처리를 위한 시퀀스 대 시퀀스 계층 입력 및 (4) 데이터 세트 내에 존재하는 장기 종속성을 학습하기 위한 시간적 자기 주의 디코더. 이러한 특수 구성 요소를 사용하면 해석 가능성도 높아집니다. 특히 우리는 TFT가 (i) 예측 문제에 대한 전역적으로 중요한 변수, (ii) 지속적인 시간 패턴, (iii) 중요한 이벤트를 식별하는 데 도움이 되는 세 가지 중요한 해석 가능성 사용 사례를 가능하게 한다는 것을 보여줍니다. 다양한 실제 데이터 세트에서 TFT가 실제로 어떻게 적용될 수 있는지와 그것이 제공하는 통찰력과 이점을 보여줍니다.
2. Related work
DNNs for Multi-horizon Forecasting: 기존의 다중 수평선 예측 방법(Marcellino, Stock, & Watson, 2006; Taieb, Sorjamaa, & Bontempi, 2010)과 유사하게 최근의 딥 러닝 방법은 자기회귀 모델을 사용하는 반복 접근 방식으로 분류할 수 있습니다(Li et al., 2019 ; Rangapuram et al., 2018; Salinas et al., 2019) 또는 sequence-to-sequence 모델에 기반한 직접 방법(Fan et al., 2019; Wen et al., 2017).
반복 접근 방식은 예측을 미래 입력에 재귀적으로 공급하여 얻은 다단계 예측과 함께 한 단계 앞서가는 예측 모델을 활용합니다. LSTM(Long Short-Term Memory)(Hochreiter & Schmidhuber, 1997) 네트워크를 사용한 접근 방식은 적층된 LSTM 레이어를 사용하여 한 단계 앞선 가우시안 예측 매개변수를 생성하는 Deep AR(Salinas et al., 2019)과 같이 고려되었습니다. 배포판. DSSM(Deep State-Space Models)(Rangapuram et al., 2018)은 LSTM을 활용하여 칼만 필터링을 통해 생성된 예측 분포와 함께 사전 정의된 선형 상태 공간 모델의 매개변수를 생성하는 유사한 접근 방식을 채택합니다. Wang et al.의 다변량 시계열 데이터용 (2019). 보다 최근에는 Transformer 기반 아키텍처가 Li et al.에서 탐구되었습니다. (2019), 예측하는 동안 수신 필드의 크기를 증가시키기 위해 로컬 처리 및 희소 주의 메커니즘을 위한 컨볼루션 레이어의 사용을 제안합니다. 단순함에도 불구하고 반복 방법은 목표를 제외한 모든 변수의 값이 예측 시점에 알려져 있다는 가정에 의존합니다. 따라서 목표만 미래 입력에 재귀적으로 공급되어야 합니다. 그러나 많은 실제 시나리오에서 사전에 알려지지 않은 많은 유용한 시변 입력이 존재합니다. 따라서 반복적인 접근 방식에서는 직접적인 사용이 제한됩니다. 반면에 TFT는 입력의 다양성을 명시적으로 설명합니다. 자연스럽게 정적 공변량과 (과거 관찰된 것과 미래에 알려진) 시변 입력을 처리합니다.
대조적으로, 직접 방법은 각 시간 단계에서 미리 정의된 여러 기간에 대한 예측을 명시적으로 생성하도록 훈련됩니다. 그들의 아키텍처는 일반적으로 시퀀스 대 시퀀스 모델에 의존합니다. 과거 입력을 요약하는 LSTM 인코더와 미래 예측을 생성하는 다양한 방법. Multi-horizon Quantile Recurrent Forecaster(MQRNN)(Wen et al., 2017)는 LSTM 또는 컨벌루션 인코더를 사용하여 각 지평선에 대해 다층 퍼셉트론(MLP)에 공급되는 컨텍스트 벡터를 생성합니다. Fan et al. (2019) 다중 모드 주의 메커니즘은 양방향 LSTM 디코더에 대한 컨텍스트 벡터를 구성하기 위해 LSTM 인코더와 함께 사용됩니다. LSTM 기반 반복 방법보다 성능이 우수함에도 불구하고 이러한 표준 직접 방법의 해석 가능성은 여전히 어렵습니다. 대조적으로, 우리는 주의 패턴을 해석함으로써 TFT가 시간적 역학에 대한 통찰력 있는 설명을 제공할 수 있고 다양한 데이터 세트에서 최첨단 성능을 유지하면서 그렇게 할 수 있음을 보여줍니다.
Time Series Interpretability with Attention: 주의 메커니즘은 번역(Vaswani et al., 2017), 이미지 분류(Wang, Jiang, Qian, Yang, Li, Zhang, Wang, & Tang, 2017) 또는 표 학습(Arik & Pfister)에 사용됩니다. , 2019) 주의 가중치의 크기를 사용하여 각 인스턴스에 대한 입력의 두드러진 부분을 식별합니다. 최근에는 LSTM 기반(Song et al., 2018) 및 변환기를 사용하여 해석 가능성 동기(Alaa & van der Schaar, 2019; Choi et al., 2016; Li et al., 2019)가 있는 시계열에 맞게 조정되었습니다. 기반(Li et al., 2019) 아키텍처. 그러나 이것은 정적 공변량의 중요성을 고려하지 않고 수행되었습니다(위의 방법은 각 입력에서 변수를 혼합하기 때문에). TFT는 기여 시간에 따라 달라지는 입력을 결정하기 위해 self-attention 외에도 각 시간 단계에서 정적 기능에 대해 별도의 인코더-디코더 주의를 사용하여 이를 완화합니다.
Instance-wise Variable Importance with DNNs: 인스턴스(즉, 샘플)별 변수 중요도는 사후 설명 방법으로 얻을 수 있습니다(Lundberg & Lee, 2017; Ribeiro et al., 2016; Yoon, Arik, & Pfister, 2019) 및 본질적으로 해석 가능한 모델(Choi et al., 2016; Guo, Lin, & Antulov-Fantulin, 2019). 사후 설명 방법, 예. LIME(Ribeiro et al., 2016), SHAP(Lundberg & Lee, 2017) 및 RL-LIM(Yoon et al., 2019)은 사전 훈련된 블랙박스 모델에 적용되며 종종 대리 해석 가능으로의 증류를 기반으로 합니다. 모델 또는 기능 속성으로 분해. 입력의 시간 순서를 고려하도록 설계되지 않았으므로 복잡한 시계열 데이터에 대한 사용이 제한됩니다. 본질적으로 해석 가능한 모델링 접근 방식은 기능 선택을 위한 구성 요소를 아키텍처에 직접 구축합니다. 특히 시계열 예측의 경우 시간 종속 변수 기여도를 명시적으로 수량화하는 것을 기반으로 합니다. 예를 들어, 해석 가능한 다중 변수 LSTM(Guo et al., 2019)은 숨겨진 상태를 분할하여 각 변수가 고유한 메모리 세그먼트에 기여하고 변수 기여를 결정하기 위해 메모리 세그먼트에 가중치를 부여합니다. 시간적 중요성과 변수 선택을 결합하는 방법도 Choi et al. (2016), 각 주의 가중치를 기반으로 단일 기여 계수를 계산합니다. 그러나 한 단계 앞선 예측만 모델링하는 단점 외에도 기존 방법은 글로벌 시간 역학에 대한 통찰력을 제공하지 않고 주의 가중치에 대한 인스턴스별(예: 샘플별) 해석에 중점을 둡니다. 대조적으로, 섹션 7의 사용 사례는 TFT가 전역 시간 관계를 분석할 수 있고 사용자가 전체 데이터 세트에 대한 모델의 전역 동작을 해석할 수 있음을 보여줍니다. 특히 지속적인 패턴 식별(예: 계절성 또는 지연 효과) 및 존재하는 제도.
4. Multi-horizon forecasting

4.1 Gating Mechanisms
외생변수와 종속변수 사이의 관계는 예측하기 어렵다. 예를 들어, 금융 데이터에서 코로나 발생과 주가 지수의 관계는 미리 예측하는 것이 불가능하다). 또한, 데이터의 노이즈가 심하거나 크기가 너무 작아 단순한 모델이 훨씬 효과적일 가능성이 높다. 따라서, TFT는 연구자가 필요한 경우에만 비선형으로 처리를 하여 모델의 유연성을 높였따. GRN(Gated Residual Network)가 그것이다. GRN은 다음에 따라 구동한다.

여기서 ELU(Exponential Linear Unit Activation Function)는 입력이 0보다 크면 Identify Function, 0보다 작을 때는 출력이 일정하며, GLU(Gated Linear Units)를 사용해 필요 없는 데이터셋을 제거한다. 1, 2는 모두 중간 층, 는 Weight Sharing Index를 의미하고, Standard Layer Normalization가 사용되었다. GLU의 수식은 다음과 같습니다.
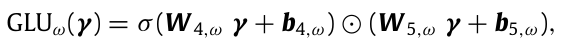
GLU의 활성화 함수는 시그모이드 함수이고, Elementwise Hadamard Product를 사용하여 연산하였다. GLU는 입력변수 a의 비선형 기여도를 바꿀 수 있다. 예컨대, GLU가 모두 0이라면 Layer를 스킵한다. GRN은 만약 Context Vector가 없는 경우 Context Input을 0으로 취급한다. dropout을 적용.
5. Model architecture
다양한 문제에 대한 높은 예측 성능을 위해 각 입력 유형(즉, 정적, 알려진, 관찰된 입력)에 대한 기능 표현을 효율적으로 구축하기 위해 표준 구성 요소를 사용하도록 TFT를 설계합니다. TFT의 주요 구성 요소는 다음과 같습니다.
1. 아키텍처의 사용되지 않는 구성 요소를 건너뛰는 게이팅 메커니즘으로 광범위한 데이터 세트 및 시나리오를 수용할 수 있도록 적응형 깊이와 네트워크 복잡성을 제공합니다.
2. 변수 선택 네트워크는 각 시간 단계에서 관련 입력 변수를 선택합니다.
3. 정적 기능을 네트워크에 통합하기 위한 정적 공변량 인코더는 컨텍스트 벡터를 인코딩하여 시간 역학을 조절합니다.
4. 관찰된 입력과 알려진 시변 입력 모두에서 장단기 시간 관계를 학습하기 위한 시간 처리. 시퀀스 대 시퀀스 레이어는 로컬 처리에 사용되는 반면 장기 종속성은 새로운 해석 가능한 다중 헤드 주의 블록을 사용하여 캡처됩니다.
5. 각 예측 범위에서 가능한 목표 값의 범위를 결정하기 위한 분위수 예측을 통한 예측 간격.
그림 2는 TFT(Temporal Fusion Transformer)의 상위 수준 아키텍처를 보여주며 개별 구성 요소는 후속 섹션에서 자세히 설명합니다.
실생활에서 대다수의 데이터가 시계열로 측정되므로 다층 시계열 분석은 데이터 분석의 효율성을 높이도록 도와준다. 그러나 다양한 종류의 정보가 갖는 이질성을 모두 반영하는 것이 관건이다. 이런 점에서 TFT는 시간 불변하는 변수와 시간에 따라 변하는 변수를 모두 모형에 반영할 수 있다는 점에서 장점이 있다. 미세먼지 농도를 다룬 데이터나 주가의 향방을 확인하는 데이터 등 시계열로 측정 가능한 다양한 분야에서 TFT가 활용되고 있다. 예측 모형의 결과는 TFT가 다른 분석 방법에 비해 매우 뛰어난 성능을 가지고 있음을 보여준다.
'Data Analysis' 카테고리의 다른 글
| [통계] 판별분석 (1) | 2023.01.25 |
|---|---|
| [통계] 이산선택모형 (0) | 2023.01.25 |
| [통계] 회귀분석 (1) | 2023.01.21 |
| [기초통계] 추정, 신뢰도 및 가설검정 (1) | 2023.01.20 |
| [통계] 확률과 확률분포 (0) | 2023.01.19 |




댓글