•개념
-설명변수를 통해 선형판별함수를 도출하여 2개 이상의 그룹을 구분 및 예측함
-등간 척도나 비율 척도로 측정된 독립변수를 이용해 명목척도 또는 서열척도로 측정된 종속변수를 분류
•종류
-종속변수의 집단수가 2개인 경우: two-group discriminant analysis
-종속변수의 집단수가 3개 이상인 경우: multiple discriminant analysis
•분류(classification)와의 차이점
1)분류: 대상이 몇 개의 그룹으로 나뉘어 지는지 자료를 보기 전까지는 모름
2)판별: 존재하는 그룹의 수를 알고 있고, 새로운 대상이 어느 그룹에 속하는지 결정
•가설
-귀무가설: 두 개 또는 그 이상의 집단의 평균이 동일하다.
-대립가설: 두 개 또는 그 이상의 집단의 평균이 동일하지 않다.
•기본 원리
-종속변수 그룹들 사이의 분산을 최대화 할 수 있는 새로운 축을 찾는 과정
-사례)
-A와 B 두 개의 그룹을 ① X1 만으로 분류할 경우 à 오 분류의 크기는 C1
-X2만으로 분류할 경우 à 오 분류의 크기는 C2
-오 분류 크기를 최소화하기 위해 새로운 함수 Z를 생성
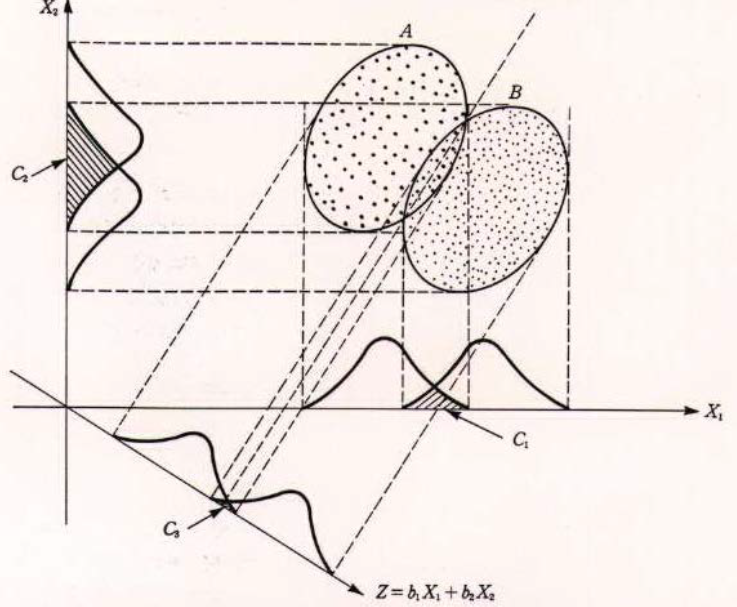
•기본 원리
-Z를 선형판별함수(linear discriminant function)이라 함
-판별함수의 목적이 종속변수의 그룹을 정확하게 분류하는 데 있다면,
1)판별함수로부터 유의적인 판별력이 있는 독립 변수들을 선택한 다음
2)분류를 위한 기준으로 판별함수로부터 계산한 판별득점(discriminant score)을 이용
-
-도출할 수 있는 판별함수의 수 = Min{(그룹수-1), 독립변수의 수}
-예를 들어, 독립변수의 수가 5개이고, 3개의 그룹이면
-Min{(3-1), 5} = 2
•LDA (Linear discriminant analysis)
-기존의 training 데이터의 class를 잘 나누는 선을 찾고 새로운 데이터가 나타났을 때 어떤 class인지 분류해주는 알고리즘
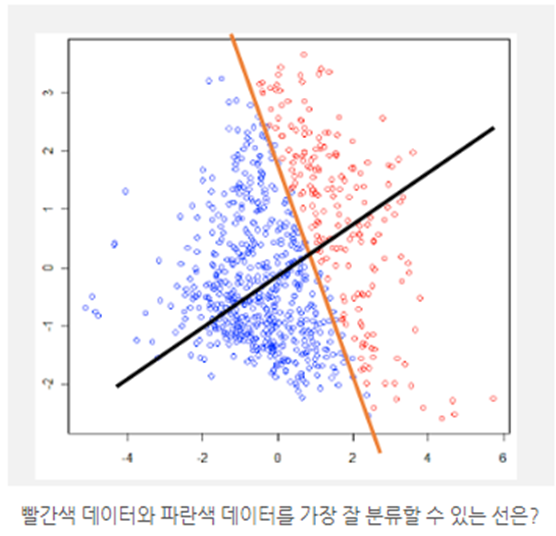
•LDA (Linear discriminant analysis)
-베이지안 정리
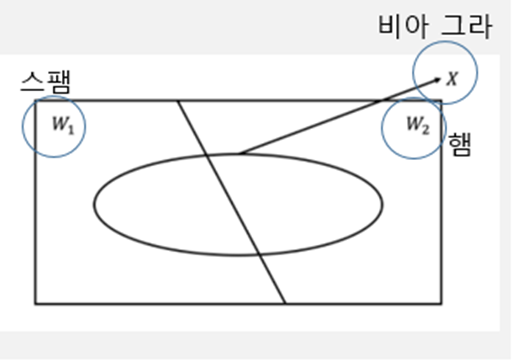
-새로운 데이터 x가 등장하면 P(W1|x)와 P(W2|x)를 각각 구하고 둘 중 전자가 크면 W1, 후자가 크면 W2로 분류

•LDA (Linear discriminant analysis)
1) 베이지안 정리

1) LDA 가정(속성변수가 1개)

-두 가정을 섞어 Pk(k)에 대입하면,
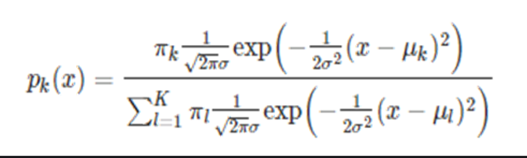
-양변에 로그를 씌우고, logPk(x)를 δk(x)로 치환하면,
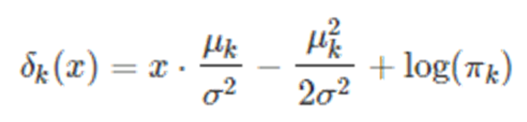
2) LDA 가정(속성변수가 2개 이상)
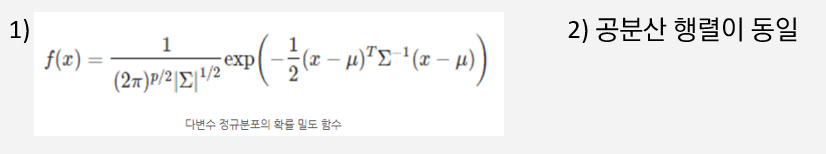
-두 가정을 섞어 Pk(k)에 대입하면,
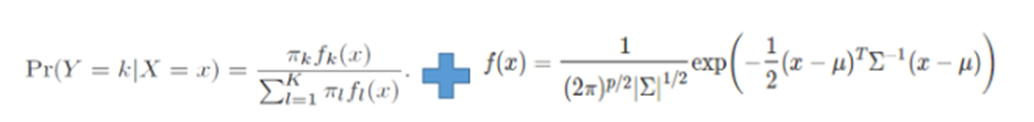
-양변에 로그를 씌우고, logPk(x)를 δk(x)로 치환하면,
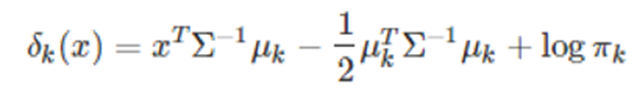
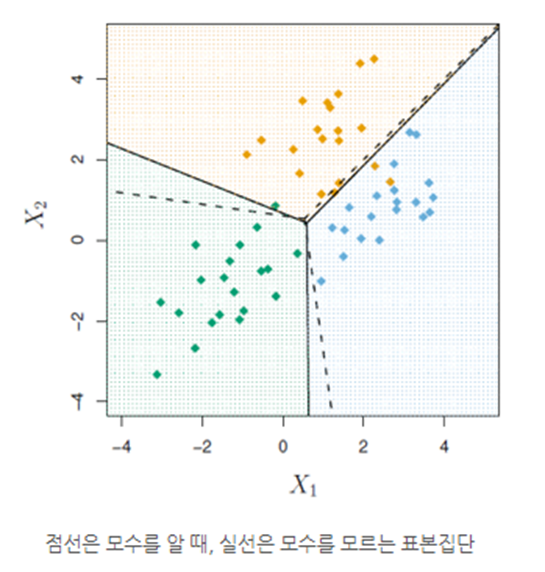
-3개의 class가 있다면 1클래스와 2클래스를 비교해서 판별식을 그리고, 2클래스와 3클래스, 3클래스와 1클래스를 비교해서 판별식을 그려준다. 아래 그림은 클래스 3개, 속성변수 2개인 경우
'Data Analysis' 카테고리의 다른 글
| [통계] 모델 검증 (0) | 2023.01.26 |
|---|---|
| [통계] 모델 선택 및 PCA (0) | 2023.01.26 |
| [통계] 이산선택모형 (0) | 2023.01.25 |
| 다중 변수 시계열 분석(Temporal Fusion Transformers) (0) | 2023.01.21 |
| [통계] 회귀분석 (1) | 2023.01.21 |




댓글