•개발된 모델이 데이터를 잘 설명하는지 평가
-학습 – 모의고사 – 시험 으로 이해
-학습 데이터로 모델을 생성한 뒤 중간과정 없이 테스트 데이터로 모델을 평가하면 과적합/과소적합이 발생할 수 있음
-모델이 이미 테스트 데이터를 학습하였기 때문에 모델 개선 후 다시 테스트할 수 있는 방도가 없음
-따라서, 중간에 Validation dataset을 만들어서 검증
•종류
-Holdout
-K-fold cross validation
-Leave-one-out cross validation (LOOCV)
•Holdout
-전체 데이터셋에서 테스트 데이터를 분리하고 남은 학습 데이터의 일부를 검증 데이터셋으로 또 분리하는 방법
-즉, 전체 데이터를 3개(학습 데이터, 검증 데이터, 테스트 데이터)로 분류

-가장 간단하지만 학습 데이터에 손실이 있기 때문에 데이터가 적은 경우 사용하기 어려움
-검증을 한 번 밖에 진행할 수 없음
•K-fold Cross validation
-Holdout 방식을 개선하기 위해 교차 검증(Cross validation, CV) 방식을 사용
-최소 2번 이상의 검증을 진행하므로 각 검증 결과의 평균을 모델의 검증 결과로 사용
-K-fold 교차검증은 데이터를 K개로 나눈 뒤 차례대로 하나씩 검증 데이터셋으로 활용하여 K번 검증을 진행
-이 방법도 학습 과정마다 학습 데이터에 손실이 있기는 하지만, 1) 전체 데이터를 다 볼 수 있고, 2) 검증 횟수를 늘릴 수 있는 장점이 있음
-다음은 K=5인 K-fold 교차검증 진행 방식(일반적으로 5 ≤ K ≤ 11 범위로 설정)

•LOOCV
-K-fold 교차 검증의 극단적인 형태로 학습 데이터셋이 극도로 작을 때 사용할 수 있는 교차검증 방법
-오직 한 개의 인스턴스만을 검증 데이터셋으로 남겨놓음(Leave-one-out)
-검증 데이터가 하나이므로 학습 데이터가 총 N개라면 총 N번의 교차 검증을 진행
-학습 데이터의 손실을 최소화할 수 있지만 샘플 데이터 수가 1,000개만 되어도 총 1,000번의 학습과 검증을 진행해야 하므로 시간과 컴퓨팅 자원이 많이 필요

•Holdout vs K-fold CV vs LOOCV

•bootstrapping
-Random sampling을 통해 training data를 늘리는 방법
-데이터 셋(training data set)의 데이터 분포가 고르지 않은 경우 주로 사용
-예를 들어, training set에 사과 이미지 1만장, 오렌지 이미지 100장이 포함되어 있다면, 항상 사과만 선택하는 질 나쁜 classifier도 99%의 트레이닝 정확도를 보일 수 있음
-이런 상황에서는 데이터가 적은 클래스의 error는 무시되는 방향으로 트레이닝 되기 쉬움
-이를 해결하기 위해 1) 가중치(weight)를 주거나, 2) bootstrapping을 이용해서 오렌지의 데이터 수를 늘리거나, 3) 사과의 데이터 수를 줄일 수 있음
-데이터 사이즈가 적을 때, Bootstrapping이 CV보다 좋은 성능을 보이는 것으로 알려져 있음
-학습 방법은 아래와 같다.
1)전체 training sample 중에서 n개를 추출하여 모델을 학습시킨다(이 때 n은 원래 학습 데이터의 크기보다 작아도 된다)
2)학습된 모델을 이용하여, training sample을 분류(classify)한다.
3)잘못 분류된 학습 데이터가 선택될 probability를 높이고, 제대로 분류된 데이터가 선택될 probability를 낮춘다. 이렇게 하면 다음 번 학습 시 “어려운” 샘플의 비율이 커진다.
4)다시 1번으로 돌아가 학습하기를 반복한다.
•Goodness-of-fit
-실제 값과 모델 예측 값을 비교하여 얼마나 잘 예측되었는지 검증
-
1)Continuous Variable
-Mean squared error (MSE): 실제 값과 예측 값 차이의 제곱에 평균을 취한 값(평균제곱 오차)
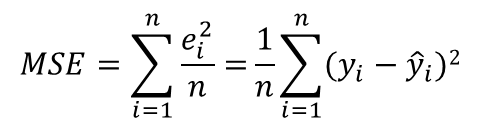
-Mean absolute deviation (MAD): 평균과 개별 관측치 사이 거리의 평균
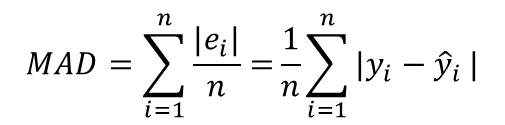
-Mean absolute percentage deviation (MAPD): 평균과 개별 관측치 사이 거리의 평균 비율
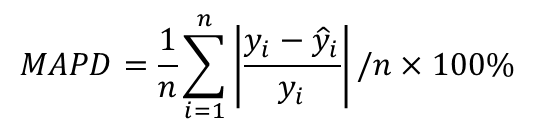
) Discrete Dependent Variable
•Confusion Matrix: 실제 자료와 예측 값을 비교
-정확도(Accuracy): 전체 데이터 중 제대로 판별한(True) 데이터의 비율
-정밀도(Precision): Positive로 에측한 인스턴스 중에 제대로 판별한 비율
-재현율(Recall): 실제 클래스가 Positive인 인스턴스를 얼마나 많이 골라냈는지 나타내는 수치. 민감도(sensitivity)라고도 함
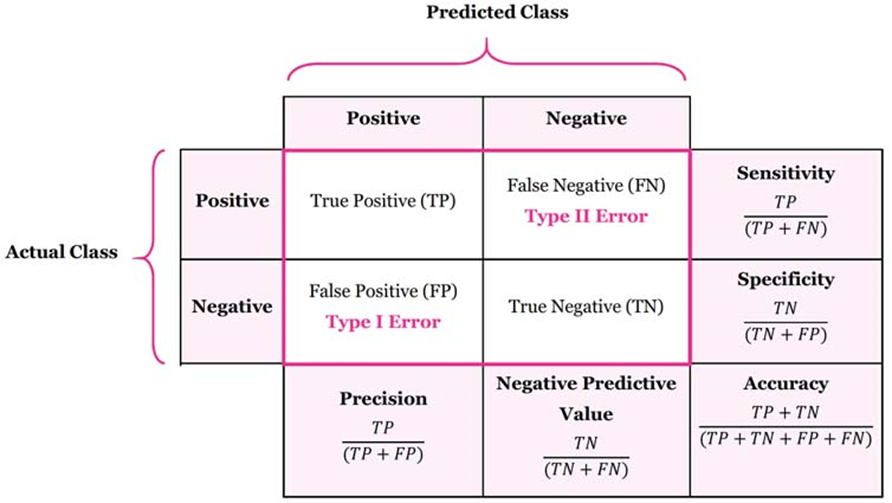
-F-score: 정밀도와 재현율 수치를 한 번에 보기 위해 만들어진 수치
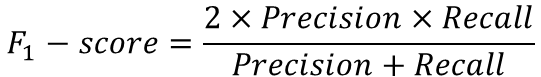
Regularization
•모형이 데이터에 지나치게 과적합하여 복잡한 형태를 띌 수 있음
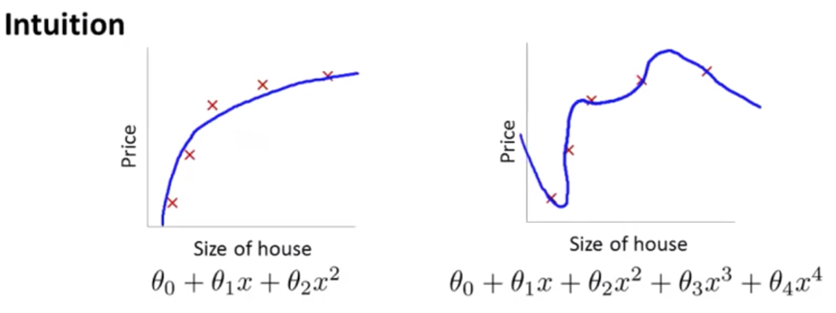
-과적합을 피하기 위해 파라미터 θ_3,θ_4 작게 만드는 페널티를 줌

Shrinkage Methods
•Shrinkage Methods
-계수 추정치를 0으로 수축(shrink)하는 기법을 사용하여 모든 설명 변수를 포함하고 있는 모델을 적합(fit)
-계수 추정치를 수축하는 것은 모델의 variance를 감소
-모델의 variance의 감소는 bias를 증가시켜 overfitting을 방지
-회귀 계수를 0으로 수축하는 방법에 대해 가장 잘 알려진 ridge regression과 lasso
•Ridge Regression
-기존의 RSS 식에 다음의 항이 추가
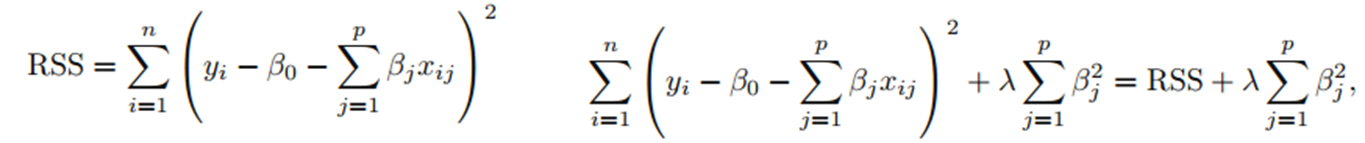
-람다는 tuning parameter이며, 위 식을 최소화하는 방향으로 모델을 학습
-아래를 수축 페널티(shrinkage penalty)라고 함
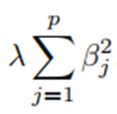
-계수 추정치가 0에 가까울수록 낮은 값을 가지므로 수축 패널티의 효과는 모든 계수 추정치가 0을 향하도록 함
-Tuning 파라미터는 두 항의 관계를 조절
- 람다가 0이면 최소제곱과 결과가 동일하고 람다가 무한이면 모든 계수 추정치가 0
- Tuning 파라미터에 따라 계수 추정치의 값이 달라지므로 람다를 선택하는 것은 중요
•Ridge Regression
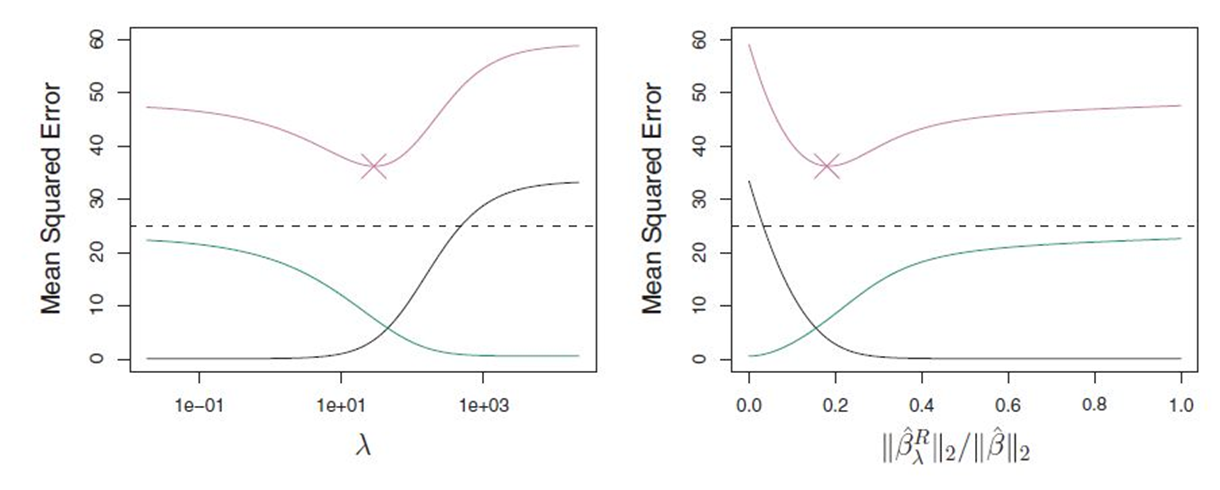
-수축 페널티를 0에서 무한까지 조절하면 편향과 분산값 사이에 절충(trade-off)가 발생
-이 둘의 합인 MSE가 최소인 지점을 찾게 되고 이때의 계수 추정치를 구함
-왼쪽 그래프는 능형회귀그래프로 bias(검정), 분산(녹색), MSE(분홍). 람다가 증가할수록 분산은 감소하고 bias는 증가. 능형회귀는 설명 변수와 반응 변수의 관계가 선형적이어서 low bias, high variance를 갖는 경우 유용.
-모델이 overfitting되면 training data가 약간만 변화해도 계수 추정치가 크게 변화하는데, 이 경우 능형회귀를 적용하여 bias를 증가시키고, variance를 감소시키는 것
•Lasso Regression
-Ridge regression의 단점을 보완하기 위해 제안된 방법
-Ridge regression은 일반적으로 변수의 부분 집합만을 포함하는 모델을 선택하는 best subset, forward stepwise, backward stepwise selection과 다르게 모든 p개의 변수를 포함하고, 패널티항은 모든 계수가 0이 되는 방향으로 수축
-하지만 람다가 무한이 아닌 경우에 계수를 정확히 0으로 수축하지 않음. 모델의 정확도 관점에서는 문제가 되지 않지만, 모델을 해석해야 하는 경우에 문제점이 발생.
-이를 해결하기 위해 라쏘의 패널티 항은 L1 norm 으로, 능형회귀와 라쏘는 패널티항이 다름

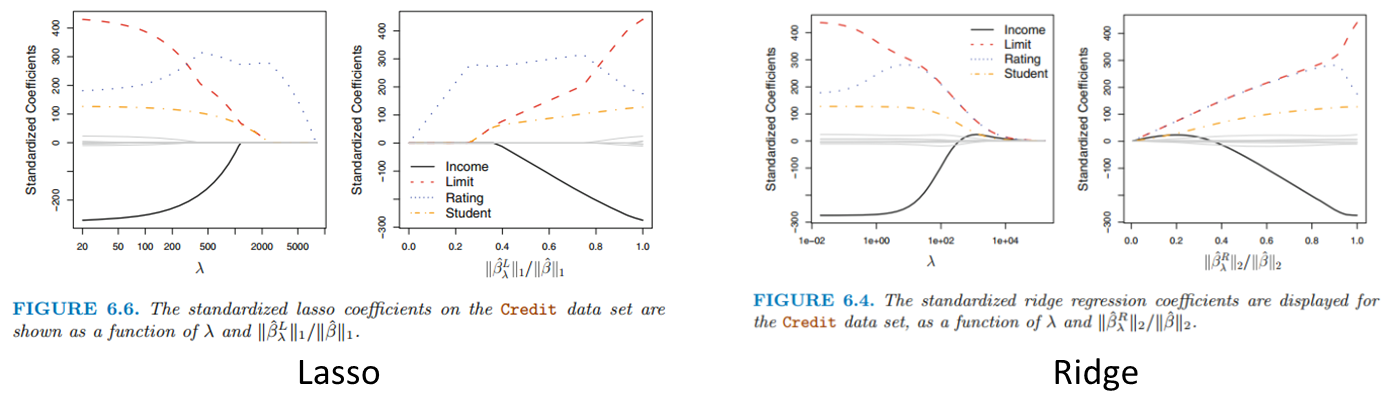
-왼쪽 그림은 람다가 0이면 기본적인 least square와 같고, 람다가 커지면 계수들이 전부 0이 되는 null model(아무 변수도 없는, y ̅를 예측하는 모델)과 같아짐
-그러나 오른쪽 그림을 보면 Ridge는 모든 계수가 완벽한 0이 되는 시점이 비슷했다면 Lasso는 Rating 계수만 남아있고 모두 0으로 수렴. 즉, 람다의 수준에 따라 몇몇 변수를 제외한 모델을 만들어 낼 수 있음
'Data Analysis' 카테고리의 다른 글
| [통계] 구조방정식(1) (0) | 2023.01.28 |
|---|---|
| [통계] 요인분석 (0) | 2023.01.27 |
| [통계] 모델 선택 및 PCA (0) | 2023.01.26 |
| [통계] 판별분석 (1) | 2023.01.25 |
| [통계] 이산선택모형 (0) | 2023.01.25 |




댓글