구조방정식이란?
•인과관계 추론을 위한 대표적인 분석기법
•직접 관찰이 불가능한 잠재변수의 측정도구(예: 설문문항)의 타당성을 확인하고, 동시에 잠재변수 간의 관계에 대해 연구자가 논리적으로 수립한 가설을 경험적으로 검정할 수 있는 강력한 분석기법
•관찰변수와 잠재변수 간의 관계를 다루는 측정모형(measurement model)과 잠재변수와 잠재변수 간의 관계를 다루는 구조모형(structural mode)을 동시에 분석
•표본에서 관찰된 공분산(행렬)과 연구모형으로 예측한 공분산(행렬)간의 차이를 가능한 한 적게 하고자 하는 분석법

구조방정식은 측정관계를 분석하는 확인적 요인분석(confirmatory factor analysis: CFA)과 구조관계를 분석하는 경로분석(path analysis)을 동시에 수행
(1) 확인적요인분석 모형(confirmatory factor analysis)
•관찰변수들에 내재된 잠재변수의 구조(즉, 측정관계)를 확인하기 위한 분석
•필요 시 탐색적 요인분석(exploratory factor analysis)도 가능

(2) 경로분석 모형(path analysis)
•현상(즉, 변수)들간에 존재하는 인과관계(즉, 구조관계)의 타당성 분석
•관찰변수들간의 인과관계도 분석 가능
•선행변수가 후행변수에 미치는 직접, 간접, 총효과 분석가능

(3) 완전구조방정식 모형(The full latent variable model)
•다수의 관찰변수들과 잠재변수간의 관계뿐 아니라(측정모형), 잠재변수와 잠재변수들간의 관계(구조모형)를 동시에 분석
•확인적 요인분석과 경로분석을 동시에 수행

구조방정식 변수

구조방정식 이론
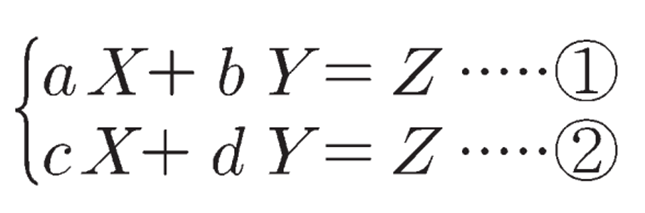
• X, Y: 내생변수
• Z: 외생변수
• a~d: 모수(parameter) – 시스템의 성질을 결정짓는 값
- 그러나 현실은 이렇게 단순하지 않고 비선형성을 띈다. 예컨대, X와 Y에 영향을 미치는 변수가 존재한다.
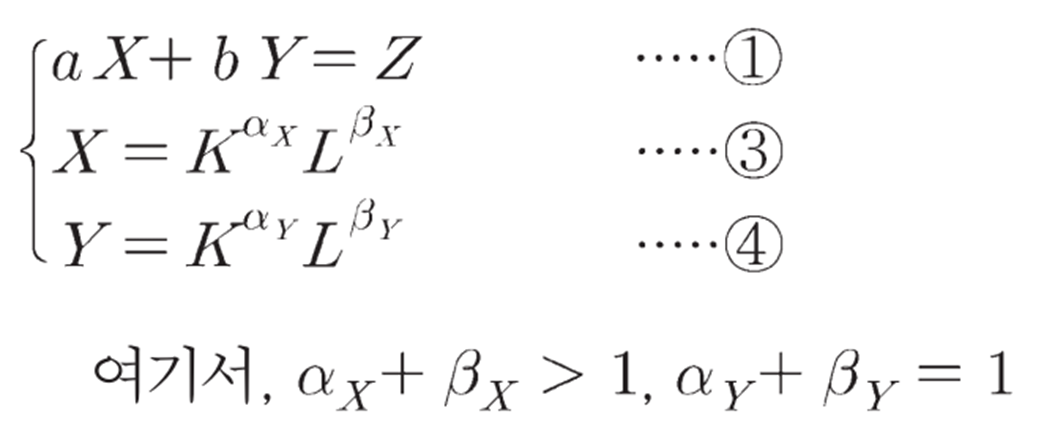
•X, Y: 내생변수, Z: 외생변수, a, b: 모수(parameter) – 시스템의 성질을 결정짓는 값
•K: 외생변수, L: K에 영향을 미치는 내생변수
- 세 가지 내생변수 X, Y, 그리고 L에 관한 세 개의 연립방정식 형태
구조방정식 모형 종합
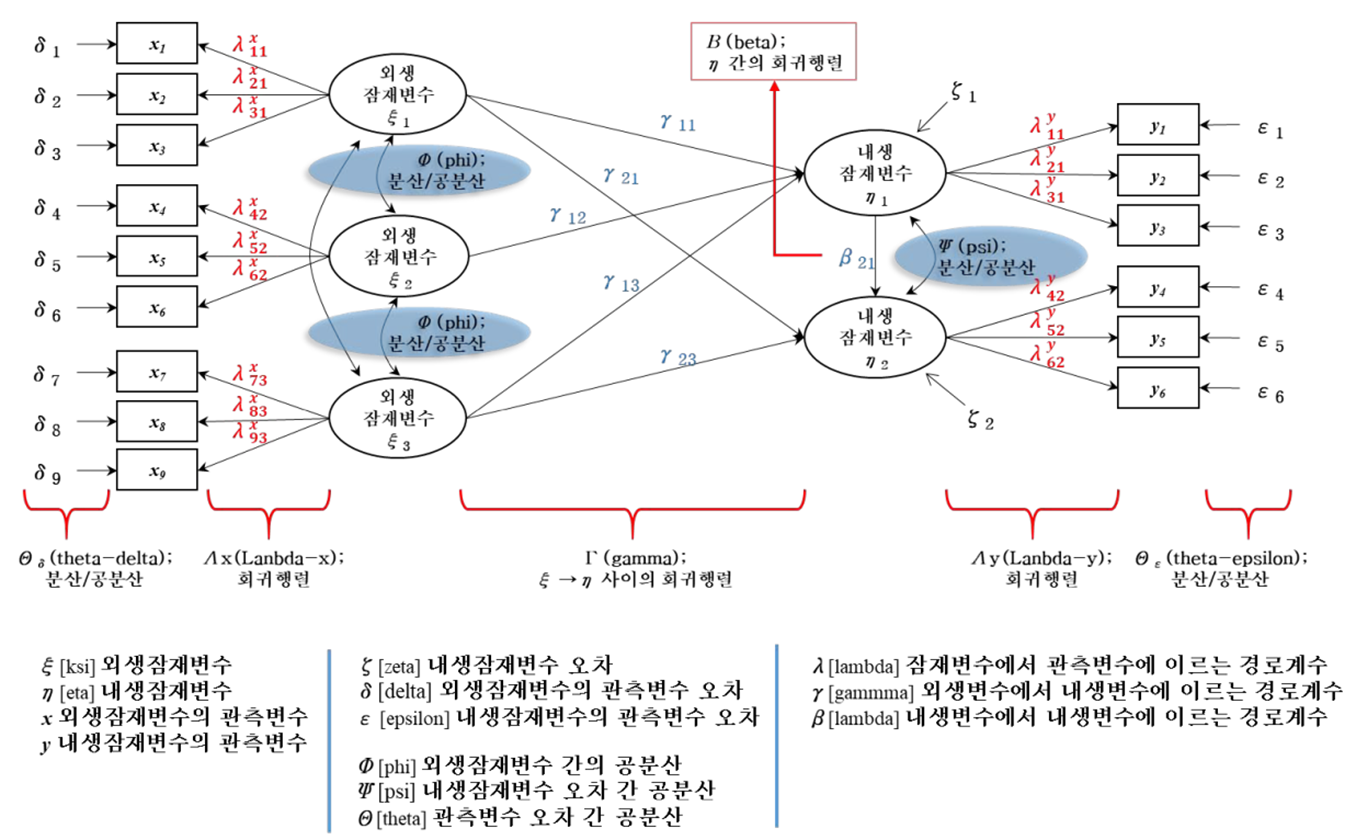
공통 요인분석
• 요인분석
- 요인분석은 많은 변수의 상호관련성을 소수의 기본적인 요인으로 집약하는 방법의 하나로 전체 변수에 공통적인 요인이 있다고 가정하고 이 요인을 찾아내어 각 변수가 어느 정도 영향을 받고 있는지 그 정도를 산출하기도 하고 그 집단의 특성이 무엇인가를 기술하려는 통계기법
- 높은 상관성을 가진 많은 변수들을 새로운 변수군으로 묶는데 초점
- 심각한 다중 공선성 문제를 해결하는데 사용
• 요인분석을 하는 이유
1) 데이터 양을 줄여 정보를 요약
2) 변수 내부에 존재하는 구조를 파악
3) 중요도가 낮은 변수를 제거
4) 측정도구의 타당성 평가
• 요인분석의 종류: 주성분 분석, 공통 요인분석
-주성분분석: 차원축소를 통해 다변량 변수들을 요약하고 변수들 간의 구조를 분석으로 변수들의 선형 결합을 통해 이루어짐
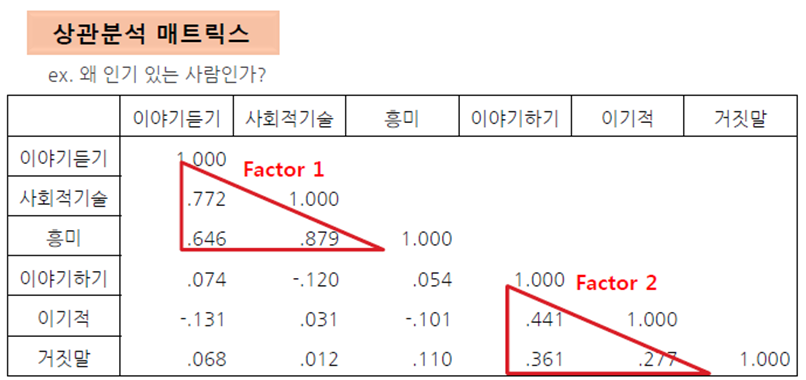
- 공통요인분석: 측정오차를 설명하기 위해 상관행렬 대각선에 있는 요소를 1 대신 공통분산으로 대체한 후 요인 적재량을 추정
- 주성분 분산은 변수의 모든 분산을 사용하므로 잠재변수와 이를 설명하는 관측변수로 이루어진 구조방정식모형에는 적절하지 않다.
• 요인분석의 종류: 주성분 분석, 공통 요인분석
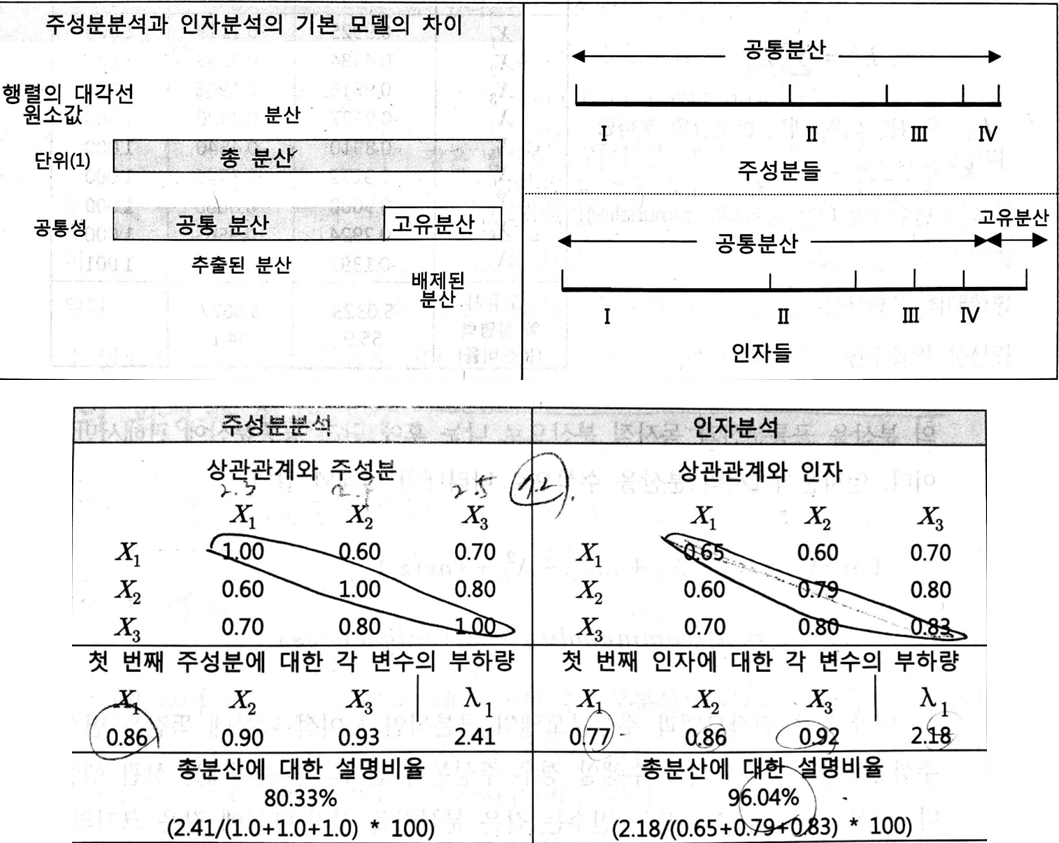
• 모든 관측변수를 대상으로 공통요인분석을 진행
• 공통요인분석 시 결정할 사항
1) 잠재 변수의 수
2) 모델 결정
- Principal component, maximum likelihood 등
- 공통요인분석은 maximum likelihood 선택
3) 회전
(1) 직각회전: varimax, quartimax, equimax 등
- 회전축이 직각을 유지하면서 회전하므로 요인들간의 상관계수가 0
- 요인들간의 관계가 상호 독립적인 경우에 사용
(2) 사각회전: oblimin 등
- 요인들이 서로 직각을 유지하지 않은채 높은 요인부하량이 더 높아지고 낮은 요인부하량은 더 낮아지도록 하는 방식
측정모델
• 측정이론: 이론모델을 구성하고 있는 구조개념(잠재변수)을 측정변수들이 얼마나 논리적이고 체계적으로 잘 나타내고 있는 가를 명시하는 것. 즉, 직접적으로 관찰되지 않는 잠재구조를 측정변수들이 얼마나 잘 명시해주고 있는가에 대한 관계를 규명하는 것 - 이론적 관계가 중요
• 측정변수는 하나의 잠재변수와만 관계를 가짐
• 관측변수와 잠재변수와의 관계: 발생하는 측정 오차를 추정해 모형에 반영
• 측정오차란 관측변수가 잠재변수를 완전하게 설명하지 못하는 정도
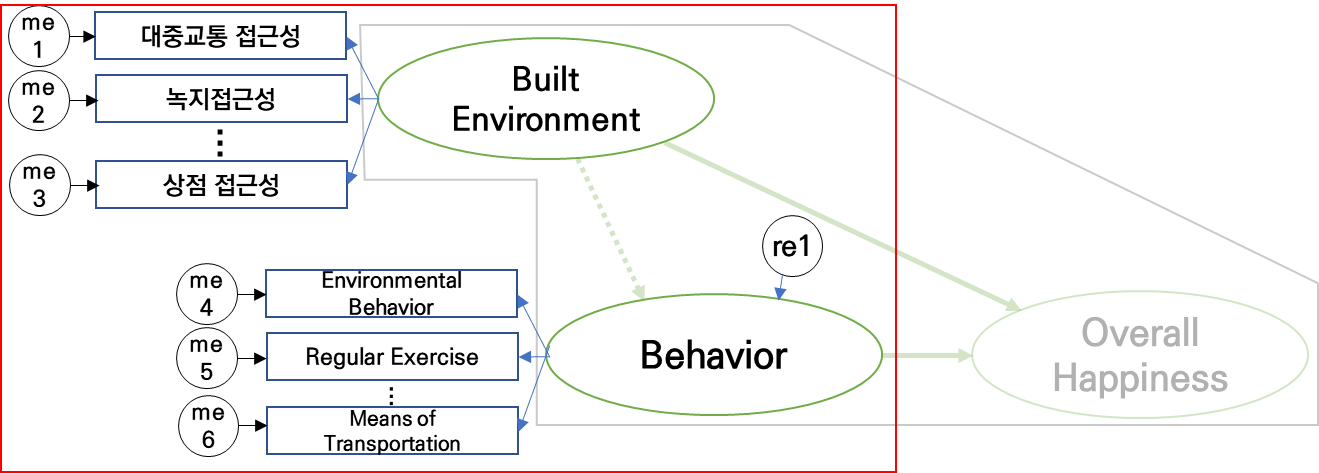
• ‘이론에 근거한 개념적 모델’이 중요
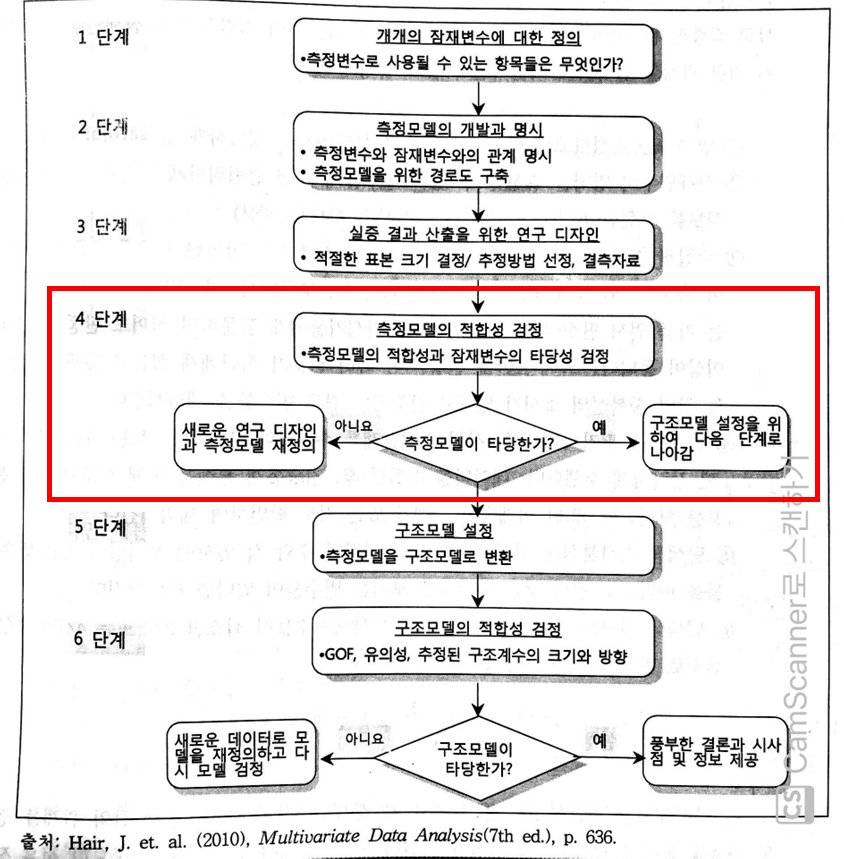
• 확인적 요인분석: 측정변수들이 얼마나 잠재변수를 나타내고 있는지 검정하는 통계분석 방법 - 측정 이론을 검정
• 확인적 요인분석을 사용해 분석: 모든 잠재변수를 대상으로 수행해야 하며, 일반적으로 전체 잠재변수를 하나의 모델로 구성하여 수행
• 확인적 요인분석을 통해 잠재변수의 단일차원성(unidimensionality), 신뢰도(reliability), 타당도(validity)를 평가할 수 있음
•단일차원성: 측정모델을 구성하는 관측변수는 오직 하나의 구성 개념만을 측정해야 한다는 특성
•단일차원성은 각각의 잠재변수가 단일요인모델(single factor model)에 의해 잘 적합되는지 평가
•적합도(fitness)는 다양한 적합도 지표를 통해 평가할 수 있음
•일반적으로 많이 사용되는 적합도 지표는 아래 표와 같음
| 구분 | 모델적합도 지표명 | 권장수준 | 참고문헌 | |
| 절대적합도 | Chisq | Discrepancy Chi Square | P-value > 0.05 | Wheaton et al. (1977) |
| RMSEA | Root Mean Square of Error Approximation | RMSEA < 0.08 | Browne and Cudeck (1993) | |
| SRMR | Standard Root Mean Residual | SRMR < 0.08 | Hu and Bentler (1999) | |
| GFI | Goodness of Fit Index | GFI > 0.9 | Joreskog and Sorbom (1984) | |
| 증분적합도 | AGFI | Adjusted Goodness of Fit Index | AGFI > 0.9 | Tanaka and Huba (1985) |
| CFI | Comparative Fit Index | CFI > 0.9 | Bentler (1990) | |
| TLI | Tucker-Lewis Index | TLI > 0.9 | Bentler and Bonett (1980) | |
| NFI | Normed Fit Index | NFI > 0.9 | Bollen (1989) | |
| 간명적합도 | Chisq/df | Chi Square/Degrees of Freedom | Chisq/df < 3.0 | Marsh and Hocevar (1985) |
• 구조방정식 모델의 적합도를 검정하는 지수들과 임계치 및 수용 수준 비교
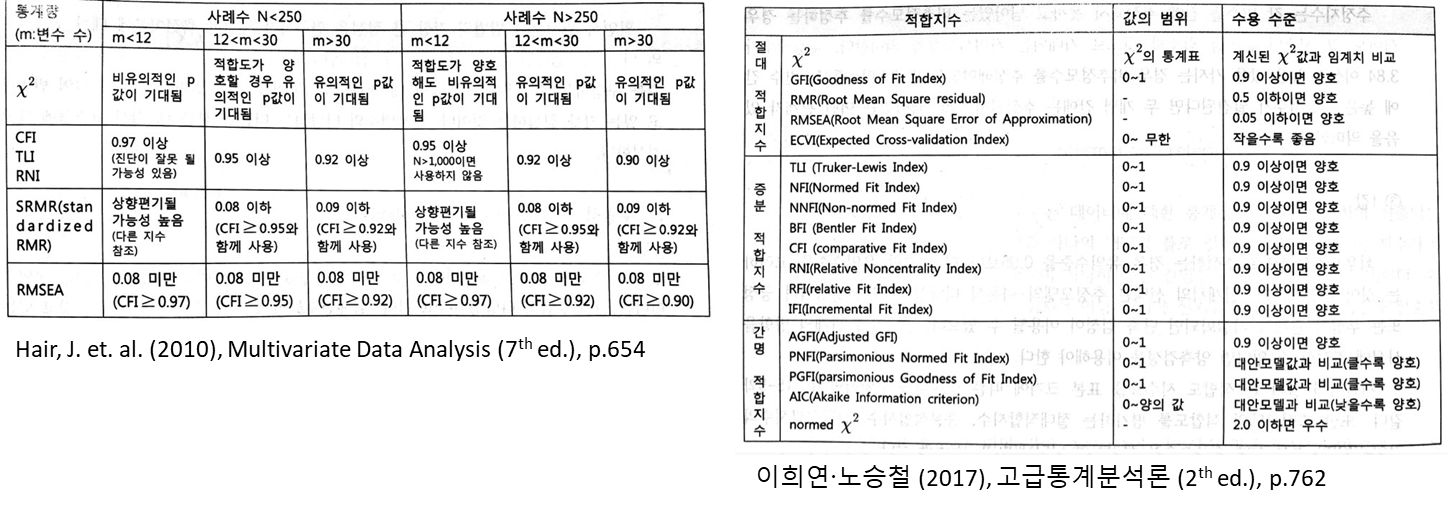
• 적합도 검정 예

• 적합도 개선
1) 관측 변수 제거
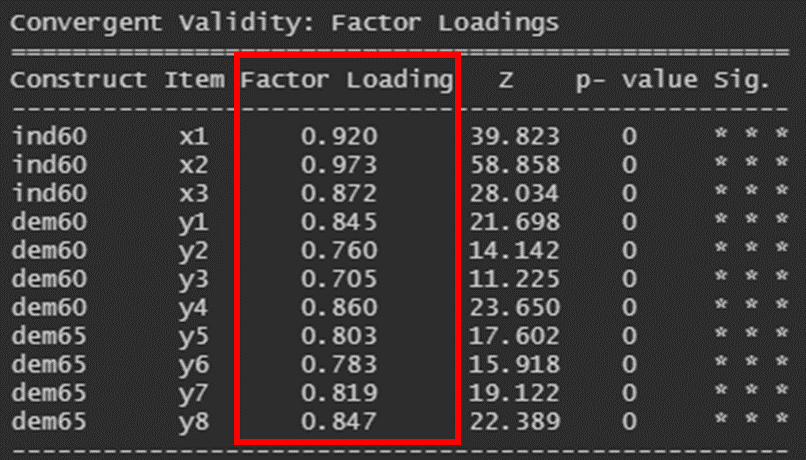
- 단일차원성 충족: 각 잠재변수에 대해 모든 관측변수가 적정 수준 이상의 요인 적재값을 가져야함 (일반적으로 0.6 이상)
- 적합도 지표를 만족하지 못하면 각 관측 변수에서 낮은 요인적재값을 갖는 관측 변수를 한 번에 한 개씩 제거
- 확인적 요인 분석을 반복 수행하면서 낮은 요인적재값을 제거해 적합도 개선
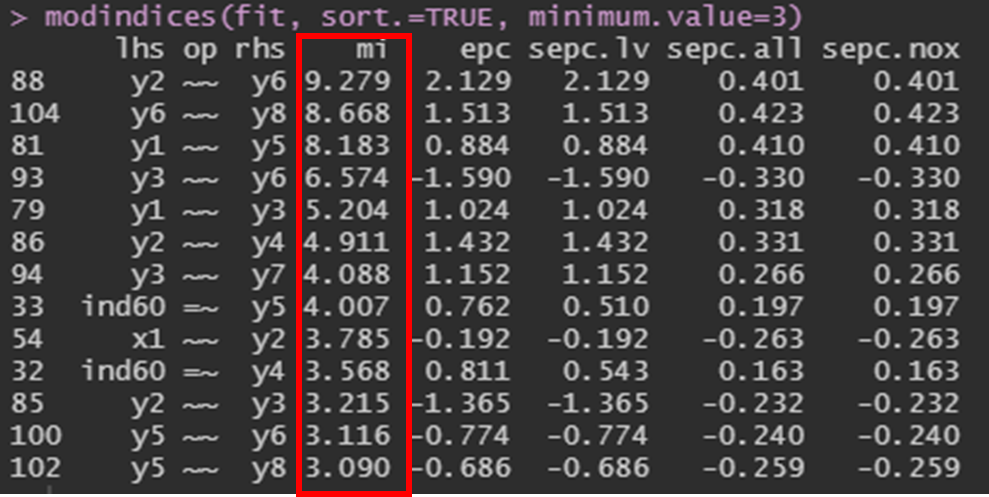
2) 수정지표(modification indices) 검토
- 수정지표에 따라 모델에 새로운 관계를 설정해 적합도를 개선하는 방법
- 쉽게 말해 각 잠재변수에 할당된 관측변수끼리 상관관계를 모형에 추가
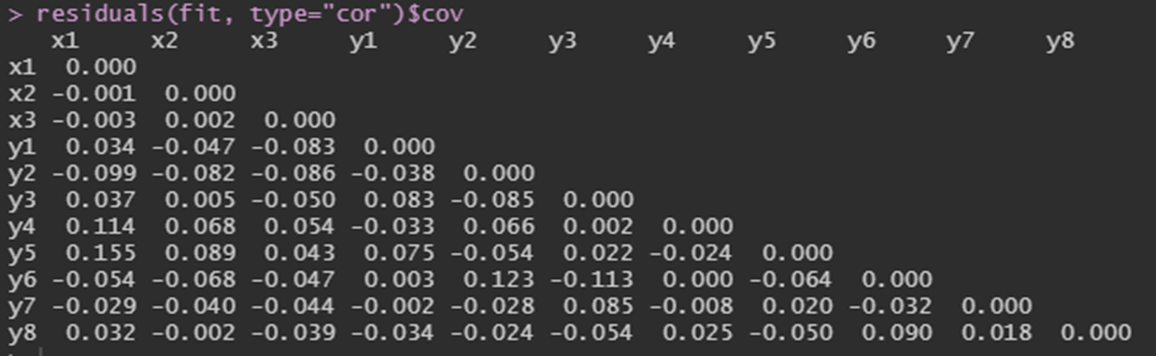
3) 잔차 분석
-측정모델은 관측변수 간의 기대된 상관관계를 표현한 것이므로 상관계수 행렬(또는 공분산 행렬)과 데이터로부터 얻은 실제 관측된 상관계수 행렬(또는 공분산 행렬) 간의 차이를 살펴보는 것 à 측정모델의 잔차
-어떤 두 변수 간 잔차가 크면 변수 간 관게에 대해 모델이 제대로 포착하지 못하는 부분이 존재한다는 것
-상관계수 잔차가 전반적으로 작을수록 이들 지표는 작은 값을 가짐
-작은 지표값은 모델의 성능이 우수하다는 것을 나타냄
'Data Analysis' 카테고리의 다른 글
| 통계, 머신러닝 및 딥러닝 소개(2) (0) | 2023.02.02 |
|---|---|
| 통계, 머신러닝 및 딥러닝 소개(1) (1) | 2023.01.31 |
| [통계] 요인분석 (0) | 2023.01.27 |
| [통계] 모델 검증 (0) | 2023.01.26 |
| [통계] 모델 선택 및 PCA (0) | 2023.01.26 |




댓글