•변수 선택이 필요한 이유
-해석이 복잡
-과적합(Overfitting) 문제 발생
-변수간 다중공선성(Multicolinearity) 발생
-데이터 분석 시간 증가
-
•해결 방안
-전 모형 탐색법(All possible subset regression)
-단계별 변수 선택
-주성분분석
•전 모형 탐색법
-변수가 P개인 경우 이를 이용해 만들 수 있는 모든 모형의 개수는 일차항만 고려할 경우 2P 개
-전모형 탐색법이란 2P 개의 모든 모형의 점수를 구하여 가장 최적의 모형을 찾는 방법을 의미
-보통 P ≤ 30일 때 사용
-
•방법
-Adjusted R2
-AIC
BIC
•회귀모형

-y: dependent variable
-x: predictor variables
-i: 1,2,…,n
-K: number of variables
-최소제곱법을 이용한 회귀 모형에서, i번째 적합값을 y ̂_i 이라고 할 때,
-전체분산
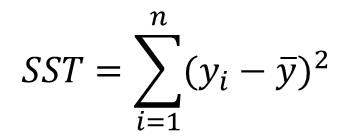
-잔차분산

•Adjusted R2
-수정된 결정계수
-기존의 결정계수가 변수가 늘어날수록 커진다는 단점을 보완
-다음과 같이 정의

-수정된 결정계수는 전체변동(SST)에 대한 잔차변동(SSE)의 비율이 포함된다는 점에서 모형 적합이 잘 되었는지를 판단하는 척도
- 따라서 수정된 결정계수 값이 높을수록 좋은 모형이라고 판단
•AIC (Akaike’s information criterion), BIC (Bayes information criterion)
-모형 선택의 기준 척도로 많이 활용
-다음과 같이 정의

-n: 데이터의 개수, p: 변수의 개수
-모형 적합 정도를 나타내는 잔차제곱합과 변수의 개수를 반영하는 벌점(penalty)항으로 이루어져 있음
AIC, BIC는 값이 더 작은 모형을 선호
•모형을 더 잘 설명하는 변수를 선택하는 방법
-전진 선택법(Forward Selection)
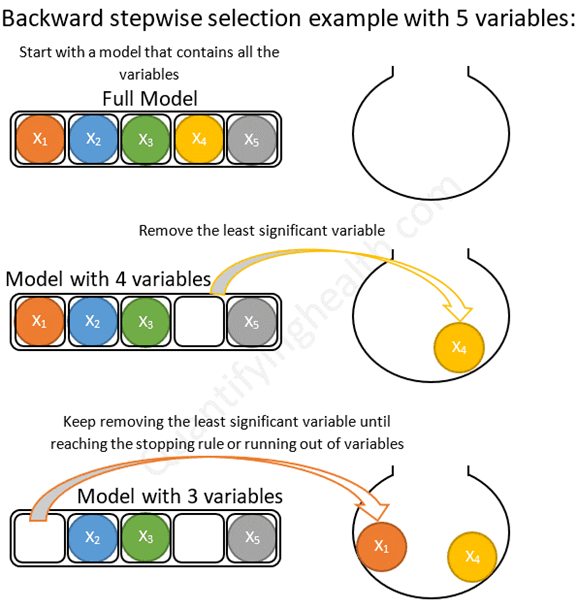
-후진 소거법(Backward Elimination)
-단계별 선택법(Forward Stepwise Selection)
•전진 선택법(Forward Selection)
-기존 모형에 설명력이 좋은 변수를 하나씩 추가하는 방법
-변수를 추가할지 말지 결정하는 유의수준을 정하고 이를 만족하면 추가
-만족하지 못 하면 선택되지 않고 종료
-가정
S: 기존 모형에 포함된 변수의 집합, S ̃: 모형에 포함되지 않은 변수의 집합
α: 유의수준
1)아직 모형에 적합시키지for 않은 변수 X_k∈S ̃를 기존 모형에 추가하여 회귀분석
2)변수 Xk에 대한 회귀계수 βk를 구하고 βk에 대한 t통계량 계산. 그리고 t통계량에 대응하는 p-value 산출. 이때, t 통계량은,

여기서 SSR(A), SSE(A)는 각각 집합 A에 포함된 모든 변수를 포함한 선형 모형의 회귀제곱합, 잔차제곱합이고 card(A)는 집합 A의 변수 개수. 또한, t 통계량은 자유도가 n-card(S)-1인 t분포를 따르므로 p-value = P(T>t), 여기서 T는 자유도가 n-card(S)-1인 t분포를 따르는 확률변수
3)이때, 최소 p-value 값과 미리 정해둔 유의수준 α 를 비교
-만약 p-value< α 이면, 최소 p-value에 해당하는 변수를 S에 포함시키고 1~2단계를 수행
-그렇지 않으면 종료
-장점: 구현 과정이 간단하고 변수가 많아도 사용할 수 있음
-단점: 한 번 선택된 변수는 모형에 계속 존재하고, 일치성(샘플수가 많아질수록 실제 모형에 수렴하는 성질)이 만족되지 않는다는 단점이 있음

•후진 소거법(Backward Elimination)
1)선형 회귀 적합
2)추정된(절편항 제외) 회귀 계수에 대해 가장 큰 p-value 산출
3)만약 p-value에 최대값이 사전에 정의한 유의수준 α보다 크면 최대 p-value에 대응하는 변수를 기존 모형에서 제외, 그렇지 않으면 종료
-장점: 구현 과정이 간단하고 변수가 많은 데이터에 적용 가능
-단점: 한 번 제외된 변수는 다시 모형에 포함할 수 없으며 일치성을 만족하지 못 함
•단계별 선택법(Forward Stepwise Selection)
1)선형 회귀 적합
2)최소 p-value와 α를 비교. 만약 p-value< α이면 최소 p-value에 해당하는 변수를 S에 포함, 그렇지 않으면 종료
3)추가된 변수를 포함하여 현재 S에 있는 모든 변수를 이용해 선형회귀 적합. 추정된 회귀변수(절편항 제외)에 대해 가장 큰 p-value 산출
4)최대 p-value 값이 사전에 정의된 유의 수준보다 크거나 같으면 해당 변수를 제외하고 반복, 그렇지 않으면 제외하지 않고 반복
-장점: 구현 과정이 간단하고 한 번 들어간 변수가 계속 포함되지 않고 변경될 수 있음(전진선택법 보완)
-단점:변수가 많아지면 계산량이 늘어나며 일치성을 만족하지 못 함
PCA 분석
•개념
-데이터의 차원 축소(dimensionality reduction)와 변수추출(feature extraction)을 위해 사용되는 방법
-변수추출은 기존 변수를 조합해 새로운 변수를 만드는 기법으로, 단순히 일부 중요 변수를 빼내는 변수선택(feature selection)과는 다름
-PCA는 기존 변수를 선형결합(linear combination)해 새로운 변수를 만듦
-예컨대, 변수가 p개, 관측치가 n개 있는 데이터 X(p x n)로 아래와 같이 새로운 변수 z를 만드는 과정
-여기에서, 벡터 xi는 데이터 행렬 X의 i번째 변수에 해당하는 행벡터(1 x n)인데, 이들을 적절히 조합해 새로운 벡터 zi (1 x n)를 만드는 것
-다시 말해, 벡터 zi는 X를 ai(p x 1)라는 새로운 축에 사영(projection) 시킨 결과물로, 변수추출로 새롭게 만들어진 zi로 구성된 행렬 Z는 아래 오른쪽 그림과 같음
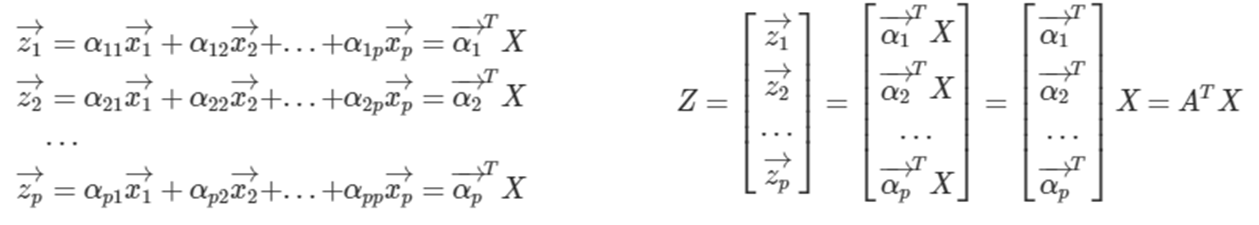
-서로 상관관계가 있는 p개의 확률변수 X1, X2, ..., Xp에 대해 주성분은 확률변수의 특정한 선형 결합
-기하학적 측면에서 보면 원래 좌표축들을 회전시켜 얻어진 새로운 좌표축을 선택하는 것
-새로운 좌표축은 변수들의 변동이 가장 큰 방향과 일치되므로 복잡한 상관구조를 단순하게 이해할 수 있음
-제1주축은 변수들 간의 공분산을 가장 많이 설명, 제2주축은 나머지 분산을 최대로 설명(직교)
변수가 3개 이상이면 n차원의 공간 상에서 주축을 추출하므로 행렬대수를 이용하여 나타냄

•사례
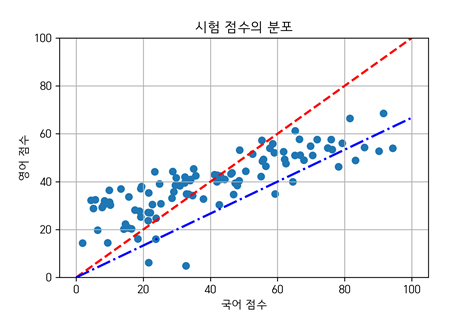
-학생 100명의 국어와 영어 시험 점수를 이용해 종합 점수를 만들 때(영어 시험이 조금 더 어려웠음),
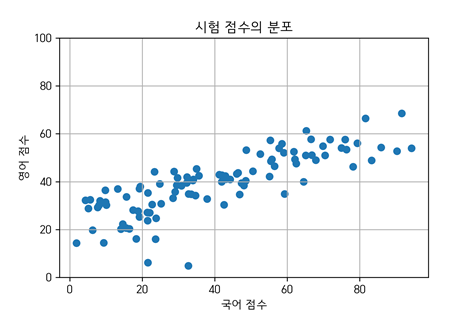
-1) 평균을 만드는 것이 가장 쉬운 방법이지만, 더 어려웠던 영어 성적에 2) 가중치를 주는 것도 가능
-예를 들어, A 학생의 국어/영어 성적이 100/80점 이라면
1)평균: 100 x 0.5 + 80 x 0.5 (red line)
2)가중치: 100 x 0.6 + 80 x 0.4 (blue line)
-최적의 가중치 행렬을 찾는 것 à 공분산 행렬을 포착
•공분산 행렬
-특징 쌍(feature pairs)의 변동이 얼마나 닮았는가(얼마나 함께 변하는가)를 나타내는 행렬
-가령 n명의 사람들로부터 각각 d개의 특징(feature)를 추출하여 이를 X로 표현
-이때, 각 열의 평균 값은 0
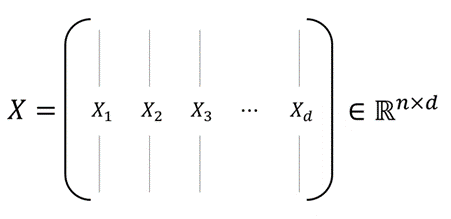
-5명의 키와 몸무게 행렬을 D라고 하면,
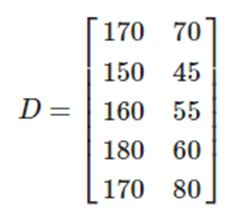
-행렬 X는 행렬 D에서 각 열의 평균을 빼서 산출

-행렬 X를 이용하여 산출한 공분산 행렬은 아래 그림
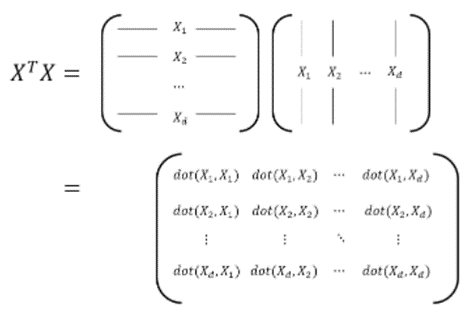
-dot(,)은 두 벡터의 내적 연산을 의미
-XTX는 i행 j열의 성분인 (XTX)ij는 d개의 feature 중
i번째 feature와 j번째 feature가 얼마나 닮았는지
모든 사람에서 값을 얻어 내적 연산을 취하여 확인
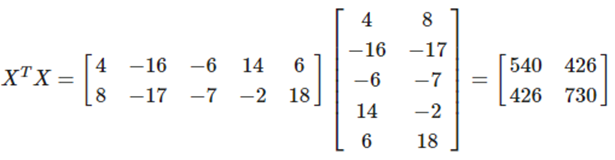
-문제는 숫자 n이 커지면 내적 값이 계속 커진다(샘플이 많으면 결과값이 더 커짐)
-따라서, n으로 나누어 문제를 해결
-이를 수학적으로
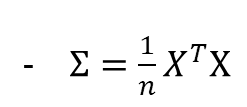
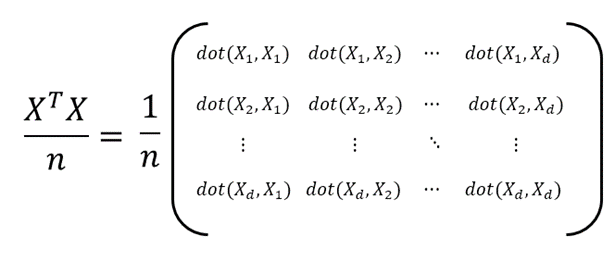
•공분산 행렬의 고유벡터
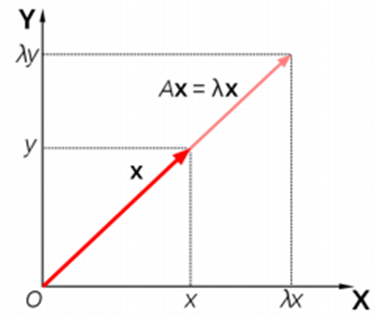
-ν를 고유벡터, λ를 고유값이라고 하면, 아래 그림과 같이 공분산행렬 A는 ν를 선형변환한다.
-Aν=λν
-즉, 임의의 점에 대해 “A”라는 transformation을 시행할 때, 고유벡터의 방향은 바뀌지 않음을 의미하며, 그 고유값은 변해지는 스케일의 정도
-(A-λI)ν=0
-고유벡터 ν가 존재하기 위해서는 (A-λI)의 역행렬이 존재하지 않음
-이 식의 판별식이 0이라는 연산을 통해 고유값과 고유벡터를 결정
•고유벡터
-T∈LM, T는 LM의 원소이며, n차원 벡터공간에서 정의된 선형사상이거나 n x n크기의 행렬을 의미
-T에 대해 상수 λ와 영이 아닌 벡터 ν가 존재할 때, Tν= λν이고, ν를 고유값 λ를 갖는 T의 고유벡터라고 함
-예를 들어,
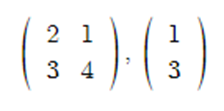
-이 둘을 곱하면,

-이는 주어진 벡터의 5배,
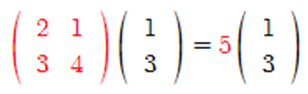
-따라서, 우리는 이 5를 벡터 (1,3)t에 대한 주어진 행렬의 고유값이라 함 à 행렬이 가진 고유한 값
'Data Analysis' 카테고리의 다른 글
| [통계] 요인분석 (0) | 2023.01.27 |
|---|---|
| [통계] 모델 검증 (0) | 2023.01.26 |
| [통계] 판별분석 (1) | 2023.01.25 |
| [통계] 이산선택모형 (0) | 2023.01.25 |
| 다중 변수 시계열 분석(Temporal Fusion Transformers) (0) | 2023.01.21 |




댓글